1.2. Sucesos
En un experimento aleatorio se llama suceso a aquello de lo que puede decirse que ha ocurrido o no. Por ejemplo en el lanzamiento de un dado podremos preguntarnos “¿Ha salido un número par?”.
Los sucesos pueden determinarse a través de una propiedad que los caracterice o, en los espacios finitos, enumerando sus elementos. Así el suceso antes mencionado “salir número par” viene descrito mediante la propiedad “ser número par”. Al lanzar un dado y observar el resultado nos preguntaremos: ¿El número obtenido es par? Si la respuesta es afirmativa el suceso habrá ocurrido y no habrá ocurrido en caso contrario. Si llamamos P al suceso “salir número par” este también podría ser descrito de forma conjuntista, enumerando sus elementos P={2,4,6}. Esta forma última de describir los sucesos es mucho más clara, pues para saber si un suceso ha ocurrido lo único que se necesita es observar si el resultado obtenido pertenece o no al conjunto.
Importante
Los sucesos suelen denotarse con letras mayúsculas, dando prioridad a aquellas que estén relacionadas con la propia definición del suceso. Por ejemplo, si hablamos del suceso "Sacar un número par", podemos denotarlo por P.
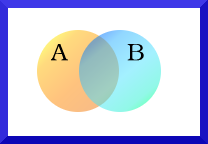
Los sucesos los podemos representar utilizando diagramas de Venn:
|
| Imagen en Wikimedia Commons de Giro720 bajo Dominio Público |
Donde A y B son dos sucesos, y el rectángulo representa el espacio muestral.
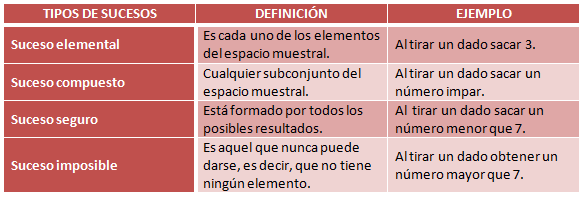
En el apartado anterior, hemos visto al "sustantivo" suceso acompañado de un "apellido", elemental, y es que podemos encontrarnos con distintos tipos de sucesos:
|
Caso de estudio
Consideramos el experimento aleatorio que consiste en lanzar un dado de seis caras, bien construido, con los números del 1 al 6 en sus caras y fijarnos en el valor que sale.
a) ¿Cuál sería el espacio muestral?
b) ¿Cuál sería el suceso "obtener número primo"?
c) ¿Y el suceso "obtener múltiplo de 3"?
d) Escribe el suceso "obtener un número de una cifra".
e) ¿Quién sería el suceso "obtener 10"?
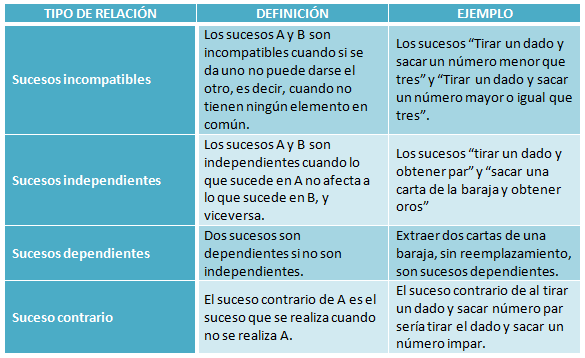
Observa el ejemplo anterior: en el espacio muestral teníamos más de un suceso ("obtener número primo", "múltiplo de 3"...). Esto implica que puedan existir relaciones entre los distintos sucesos.
|
Caso de estudio
Indica qué tipo de relación existe entre los sucesos representados mediante los siguientes diagramas:
 |
| Diagrama 1 |
 |
| Diagrama 2 |