1.1. Experimentos aleatorios y espacio muestral
Probabilidad y fenómenos aleatorios
Probabilidad es una palabra que utilizamos con mucha frecuencia, y si tienes dudas de esta afirmación solo hay que echar un vistazo a la prensa diaria, de la que a continuación te ponemos unos ejemplos de titulares:

|
Pero, ¿qué tienen en común estos titulares, sin tener en cuenta la palabra probabilidad? Si te fijas cada uno pertenece a un ámbito de la actualidad, pero en ninguno conocemos de antemano cuál será el resultado. Y es que la idea de probabilidad está íntimamente ligada al concepto de azar y aleatoriedad.
Actividad
La Probabilidad es una rama de las Matemáticas que estudia los fenómenos aleatorios.
Ejemplos de experimentos aleatorios son el lanzamiento de un dado (alea en latín) o la edad media de las personas que subirán al autobús en la próxima parada. Por el contrario, la temperatura de fusión del hielo y la aceleración de la gravedad en un determinado punto de la Tierra son constantes en fenómenos deterministas. Hay también fenómenos que, aunque en principio, podría pensarse que son deterministas, la cantidad de variables que intervienen en los mismos hace imposible su predicción cierta (¿si está nublado implica que llueve?).
AV - Pregunta de Elección Múltiple
Solution
Solution
Solution
Solution
Espacio muestral y sucesos elementales
Siempre que nos encontramos en una situación que depende del azar, antes de realizarla no podemos saber a ciencia cierta qué resultado vamos a obtener, pero siempre tendrá que estar entre un conjunto de valores que sí podemos conocer.
Por ejemplo, antes de empezar la liga no podemos saber quién va a ganar en Primera División (aunque conozcamos estadísticas de los que la ganaron los últimos años), pero es seguro que el ganador tiene que ser uno de los equipos que juegan en esa división.
Importante
Se llama espacio muestral al conjunto de todos los posibles resultados de un experimento aleatorio. Lo denotaremos por E.
Cada uno de estos resultados recibe el nombre de suceso elemental.
Los espacios muestrales se visualizan mediante cajas en cuyo interior están los elementos. Por ejemplo el espacio muestral del experimento aleatorio que consiste en el lanzamiento de un dado sería:
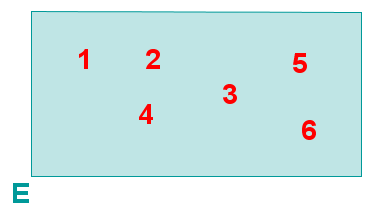
|
Experimentos aleatorios compuestos
Ya hemos visto experimentos aleatorios consistentes en tirar un dado o una moneda que se denominan experimentos aleatorios simples.
Un experimento compuesto es aquel que puede descomponerse en dos o más experimentos aleatorios simples, como el lanzamiento de varias monedas, dados, o la observación de varias características de un mismo colectivo...
Muchos experimentos compuestos consisten en sucesivas extracciones (de una baraja, urna, colectivo…).
Las hay de dos tipos:
- Extracciones con reemplazamiento. Tras cada extracción el elemento extraído se devuelve al contenedor (mazo, urna, colectivo…). De esta manera, cada extracción se realiza en las mismas condiciones que la precedente.
- Extracciones sin reemplazamiento. Tras cada extracción el elemento extraído no se devuelve al contenedor (mazo, urna, colectivo…). Cada extracción viene condicionada por las anteriores, es decir, cada vez tenemos menos elementos.
Para visualizar los espacios muestrales de los experimentos aleatorios compuestos se utilizan las tablas rectangulares (en las extracciones con reemplazo) y los diagramas en árbol, que verás después del ejercicio resuelto en un vídeo.
Caso de estudio
Escribe los espacios muestrales de los siguientes experimentos e indica si son simples o compuestos:
a. Sacar una carta de una baraja española (sin ochos ni nueves).
b. Lanzar una moneda.
c. Lanzar una moneda dos veces.
d. Sacar una bola de una caja que contiene 3 bolas rojas, dos azules y una negra.
Para terminar, un vídeo de youtube de juanmemol, que resume todos estos conceptos y que te servirá para afianzarlos: