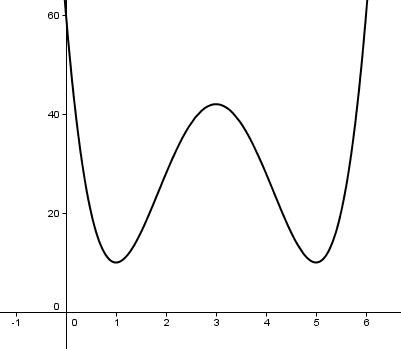
4.1. Monotonía
Importante
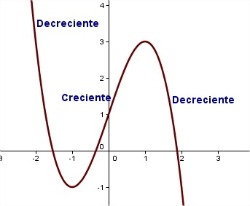
Imagen de elaboración propia |
-
Decimos que una función
es creciente si al dibujar su gráfica de izquierda a derecha el trazo cada vez es más alto. Por tanto, es creciente si al tomar dos valores 
y 
cualesquiera, si 
entonces 
.
-
Decimos que una función es decreciente si al dibujar su gráfica de izquierda a
derecha el trazo cada vez es más bajo. Por tanto, es decreciente si al
tomar dos valores
y cualesquiera, si entonces 
.
Lo normal es que la función no sea siempre creciente o decreciente sino que se alternen los intervalos de crecimiento y decrecimiento.
Ahora nos interesa que observes la siguiente ventana en la que hay representada una función y la tangente en un punto cualquiera. Como recuerdas del tema anterior la pendiente de la tangente en un punto coincide con la derivada de la función en ese punto. Queremos que recorras la función y observes el signo que tiene la pendiente de la tangente cuando la función crece y cuando decrece.
Escena de mduran bajo dominio público.
A partir de lo anterior podemos deducir lo siguiente:
Importante
Si la función f(x) verifica en un punto x=a que su derivada es positiva, f'(a)>0, la función es creciente en dicho punto.
Analogamente, si la derivada es negativa, f'(a)<0, la función es decreciente en x=a.
Por lo tanto, para saber cuándo una función es creciente o decreciente basta estudiar los intervalos en los que la función derivada es positiva o negativa.
Caso de estudio
.
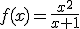Caso de estudio
|
A veces, contactan con la empresa de Ángela y Andrés para que se encarguen del estudio de una parte de un proyecto más grande. Eso les ocurrió cuando se construyó la nueva terminal del aeropuerto de Barajas en Madrid: la T4.
Le pidieron que hicieran un estudio sobre el recorrido de las brisas creadas por los aires acondicionados en lo que iban a ser los techos de la terminal. Para ello tenían que estudiar los intervalos de crecimiento y decrecimiento de la función que, inicialmente, iban a seguir las volutas del techo.
Si la función se acercaba a la de expresión 
, halla los intervalos en los que crece y decrece.
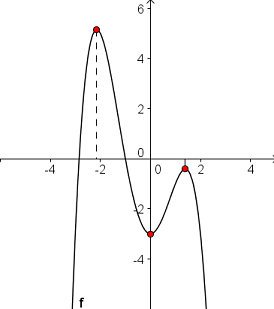
Imagen de elaboración propia |
En el tema anterior has aprendido a derivar una función, pero ¿para qué sirve derivar? Como has visto a lo largo de todo el curso, hemos intentado enseñarte las aplicaciones prácticas de todo lo que estás estudiando, y esta vez no iba a ser menos.
Ya conoces alguna de las aplicaciones, como puede ser averiguar la ecuación de la velocidad de un móvil derivando la del espacio que recorre, o la ecuación de la aceleración a partir de la velocidad. En este tema veremos otras aplicaciones.
Si ves la gráfica de la derecha, podrás decirme aproximadamente cuándo crece, cuándo decrece, o en qué puntos alcanza los valores más altos o más bajos. Es algo relativamente sencillo si tenemos la gráfica delante.
Pero, ¿y si no tuviéramos la gráfica?, ¿y si solo te dijera que esa gráfica corresponde a la función
|
y te pidiera exactamente el momento en el que se alcanzará el máximo valor?
Para ello utilizaremos las derivadas.
El crecimiento y el decrecimiento de una función es algo que ya hemos estudiado antes ¿lo recuerdas? Básicamente una función es creciente si, al aumentar la variable independiente, x, también aumenta el valor de la función, f(x). Es decreciente, si al aumentar el valor de x, disminuye el de f(x). No olvides que las gráficas se "leen" de izquierda a derecha.
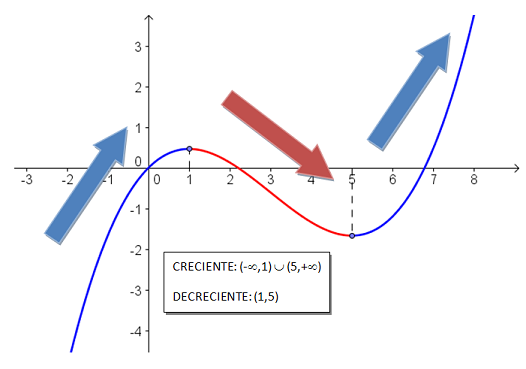
Imagen de elaboración propia |
Veamos un ejemplo real: las siguientes gráficas representan la velocidad y la aceleración de un coche. Si te fijas en la primera gráfica, la velocidad aumenta hasta el minuto 10 y comienza a disminuir desde entonces.
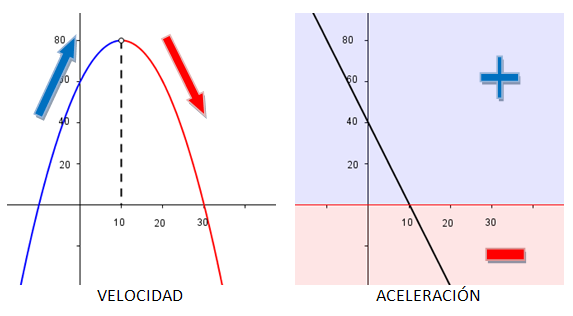
Imagen de elaboración propia |
Mira ahora la gráfica de la aceleración ¿qué ocurría hasta el minuto 10? Que la aceleración era positiva (pues su gráfica queda por encima del eje de abscisas), y si la aceleración es positiva quiere decir que el coche acelera y por tanto su velocidad aumenta.
A partir del minuto 10, la aceleración es negativa (su gráfica queda por debajo del eje de abscisas), por tanto está decelerando y la velocidad disminuye.
Seguro que en física has estudiado que la aceleración es la derivada de la velocidad. Acabamos de ver una relación entre el signo de la aceleración, y el crecimiento y el decrecimiento de la velocidad. Esta misma relación se da entre cualquier función derivable, y su derivada.
Importante
Cuando hablamos de monotonía, nos estamos refiriendo al comportamiento de una función respecto a su crecimiento o decrecimiento.
Sea f una función derivable en un intervalo (a, b), entonces es:
- Creciente en el intervalo (a,b) si f'(x) ≥ 0 en todo el intervalo (a,b)
- Decreciente en el intervalo (a,b) si f'(x) ≤ 0 en todo el intervalo (a,b)
En la siguiente escena de GeoGebra de Saúl Valverde Pérez tienes dos ejemplos, una función polinómica y una racional, en las que puedes comprobar que se cumple lo que acabamos de ver.
| f(x) función (continua) |
f ' (x) función derivada (discontinua) |
| Creciente (azul) | Positiva (azul celeste) |
| Decreciente (rojo) | Negativa (rojo) |
Como ya hemos comentado, lo relevante del importante anterior, es que ya no es necesario dibujar la gráfica para estudiar la monotonía. A continuación tienes un ejercicio resuelto por Saúl Valverde Pérez para que veas cómo hacerlo. Después hay uno que tendrás que resolver tú.
AV - Actividad de Espacios en Blanco
En una empresa están teniendo pérdidas económicas, por lo que deciden poner en marcha una serie de medidas a lo largo de los próximos 6 meses con las que pretenden remontar y obtener beneficios al finalizar dicho periodo.
Según sus cuentas, los beneficios obtenidos por la empresa al poner en marcha el plan vienen dados por la función
|
donde x es el número de meses.
Vamos a comprobar si con este plan de medidas la empresa mejorará los beneficios. Para ello tendrás que estudiar los intervalos de crecimiento y decrecimiento de los beneficios de la empresa.
