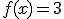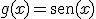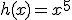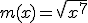2.1. Reglas de derivación. Aplicaciones al cálculo de derivadas

Actividad

A continuación en el siguiente documento te ofrecemos un listado en el que aparece una función y al lado aparece su función derivada. Todos los resultados que aparecen en esta tabla son fruto de aplicar la definición de derivada de una función. Esta otra tabla que te presentamos a continuación más abajo hace referencia a como se obtiene la derivada de la suma, resta, producto, producto por un número y cociente de funciones.

 

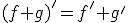
Suma (f+g)'=f'+g' La derivada de la suma de funciones es la suma
de las derivadas de estas funciones.
Resta 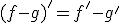(f-g)'=f'-g' La derivada de la diferencia de funciones es la
diferencia de las derivadas de estas funciones.
Producto
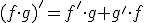 		(f \cdot g)'=f' \cdot g+g' \cdot f La derivada del producto de dos funciones es igual
a la derivada de la primera por la segunda sin derivar
más la segunda derivada por la primera sin derivar.
Cociente
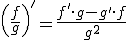 		\left( \frac{f}{g} \right )'=\frac{f' \cdot g - g' \cdot f}{g^2} La derivada del cociente de dos funciones es igual a la
derivada del numerador por el denominador sin derivar
menos la derivada del denominador por el numerador sin
derivar, y todo ello dividido por el denominador al cuadrado.
Producto por un número 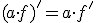(a \cdot f)'=a \cdot f' La derivada del producto de un número real por la función
es igual al número real por la derivada de la función.

Para no tener que recurrir una y otra vez a la definición, es conveniente aprenderse las reglas contenidas en esta tabla y el documento que te enlazamos más arriba, la mejor manera no es aprendérselas de memoria, sino familiarizarse con la mismas a base de practicar el cálculo de derivadas, para ello en este apartado te vamos a ofrecer unos cuantos ejemplos.

Veamos unos ejemplos en la siguiente presentación de Patricia_Perez.
La mejor forma de aprender a derivar es derivando, así que aquí tienes unos videos del Profesor de la Escuela Técnica Superior de Ingeniería Juan Medina Molina en su canal de YouTube. Quizás sea una buena idea que pinches para verlos en pantalla completa o pinchando sobre ellos para verlos en la página de youtube:
Derivada de un monomio Derivada de una exponencial


 

Derivada de un polinomio

 

Derivada de un producto



 

Derivada de un cociente

 

Derivada de una composición



 

Derivada de una composición (II)

 

Derivada de una composición (III)



 

Reflexión

En la ventana interactiva, a la que accedes desde el siguiente enlace, vas a poder practicar realizando distintas derivadas.

 

 

Derivadas de funciones

Actividad

A la derivada de una función también se la denomina derivada primera. Si volvemos a derivar la derivada primera de una función, obtenemos la llamada derivada segunda; la derivada de la derivada segunda se denomina derivada tercera; y así sucesivamente. Estas son las llamadas derivadas sucesivas de una función:

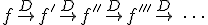
f \overset{D} \rightarrow f' \overset{D} \rightarrow f'' \overset{D} \rightarrow f''' \overset{D} \rightarrow \ \cdots

Caso de estudio

¿Existen otras funciones que a partir de alguna de sus derivadas sucesivas siempre se repitan?

Reflexión

Calcula la derivada de las siguientes funciones:

  1. f(x)=3
  1. g(x)=\begin{verbatim}sen\end{verbatim}(x)
  1. h(x)=x^5
  1. m(x) = \sqrt{x^7}

Reflexión

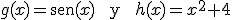Dadas las funciones g(x) = \begin{verbatim}sen\end{verbatim} (x)\begin{verbatim} y \end{verbatim}h(x) x^2+4  Calcula la derivada de la suma y el producto de ambas.

Ejemplo o ejercicio resuelto

Todos sabemos que la caída de pelo es mayor en unas épocas que en otras, pero... ¿y su velocidad de crecimiento? ¿nos crece más el pelo en unos meses que en otros? Supongamos que la longitud de nuestro pelo viene determinada por la función:

donde t, indica el tiempo en meses.

¿Cuál será la velocidad de crecimiento en febrero (mes 2)? ¿Y en julio? ¿Cuál es la función que nos da la velocidad de crecimiento en función del tiempo?