4.1 Distribuciones puntuales de carga. Cargas suspendidas

Imagen de elaboración propia

Las distribuciones de carga, sometidas al principio de superposición pueden ser de dos tipos:

1) Puntuales; una colección de cargas individuales situadas en el espacio.

2) Continuas; las cargas se encuentran uniformemente distribuidas en un volumen, superficie o hilo.

Verás algún ejemplo de distribuciones continuas de carga en los temas siguientes de esta Unidad. En este apartado, sin embargo, nos vamos a centrar en distribuciones puntuales de carga tomando alguna disposición geométrica sencilla. Ten en cuenta que, en este tipo de distribuciones, lo más complicado no es calcular las fuerzas que actúan, sino trabajar correctamente con la geometría que presentan.

Ejemplo o ejercicio resuelto

Ej resuelto distribución puntual de cargas

Imagen de elaboración propia

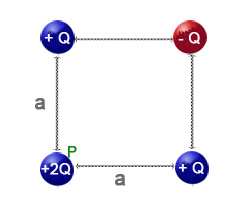
Dada la siguiente distribución puntual de cargas, calcula la intensidad de la fuerza experimentada por la carga situada en el punto P.

Retroalimentación

Solución Ej. resuelto distribución cargas

Imagen de elaboración propia

Las fuerzas ejercidas por el sistema se muestran en la figura.

Según el principio de superposición la fuerza sobre la carga de situada en el punto P será igual a la suma vectorial de las fuerzas de interacción que ejercen sobre ella todas las demás:

De estas tres fuerzas, F₂ y F₃están orientadas en las direcciones de los ejes mientras que F₁deberá descomponerse en sus dos componentes coordenadas F_1x y F_1y.

Las fuerzas entre cargas se calculan según la Ley de Coulomb, teniendo en cuenta que como el problema no da valores numéricos se trabajará de forma simbólica.

Aplicando Pitágoras se calcula que la distancia entre la carga en P y la de -Q es de √2·a

Por tratarse de una distribución cuadrada, el ángulo que forma F₁ es de 45º, por lo que las componentes F_1x y F_1ytoman sendos valores:

F_1x = F₁·cos 45º = (√2/2)·F₁

F_1y = F₁·sin 45º = (√2/2)·F₁

Mientras que, para las fuerzas con las otras dos cargas:

Efectuando la suma vectorial de las fuerzas, se llega a la solución

Resultando una fuerza diagonal en dirección suroeste, tal y como cabía esperar por la simetría del problema. Su intensidad es:

AV - Reflexión

Ejercicio distribución puntual de cargas

Imagen de elaboración propia

Tres cargas puntuales de 2 µC, 7 µC, y -4 µC respectivamente, están situadas en las esquinas de un triángulo equilátero de 0.5 m de lado.

Calcula la fuerza que experimenta la carga de 7 µC.

Retroalimentación

Imagen de elaboración propia

Según el principio de superposición la fuerza resultante es la suma vectorial de las fuerzas individuales entre cada carga. Para este problema en concreto, las fuerzas son las indicadas en la figura.

Las fuerzas entre cargas se calculan según la Ley de Coulomb:

Por tratarse de un triángulo equilátero, los ángulos de cada fuerza respecto a la horizontal y la vertical serán siempre de 60º, por lo que resulta sencillo calcular sus componentes:

F_1x= F₁·cos 60º = 0.504·0.5 = 0.252 N

F_1y= F₁·sin 60º = 0.504·0.87 = 0.436 N

F_2x= F₂·cos 60º = 1.008·0.5 = 0.504 N

F_2y= F₂·sin 60º = 1.008·0.87 = 0.873 N

Y las componentes de la fuerza resultante son por tanto

F_x = F_1x+ F_2x= 0.252 + 0.504 = 0.756 N

F_y = F_1y- F_2y= 0.436 - 0.873 = -0.436 N

Resultando su intensidad:

Siendo el ángulo formado respecto a la horizontal

Imagen de elaboración propia

Un tipo de problemas interesantes relativo a las distribuciones puntuales de carga es el referido a los cuerpos cargados que se encuentran suspendidos de un cable.

El interés de este tipo de problemas es que combinan el estudio del campo gravitatorio de los sistemas dinámicos clásicos con la presencia de una interacción de tipo electrostático. Este es el caso de los dispositivos como el electroscopio, que habías visto en el apartado 1.1 de este tema.

Un modelo simplificado de electroscopio consiste en dos pequeñas esferas de masa m cargadas con cargas iguales Q del mismo signo que cuelgan de dos hilos de longitud d, tal como se muestra en la figura. A partir de la medida del ángulo θ que forma una de las esferas con la vertical, es posible calcular el valor de su carga Q.

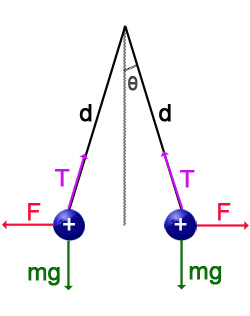
Observa que, sobre cada una de las esferas, actúan tres fuerzas:

- El peso (mg)

- La tensión de la cuerda (T)

- La fuerza de repulsión eléctrica entre las esferas cargadas (F)

Se trata de un problema clásico de equilibrio de fuerzas como los que ya pudiste estudiar en Física y Química de primero de bachillerato. El sistema evolucionará hasta que encuentre la posición de equilibrio, en la que las fuerzas se igualarán en cada uno de los ejes. Observa que, debido a la simetría del sistema, basta con estudiar el equilibrio de una de las esferas, pues la otra experimenta exactamente las mismas fuerzas.

En el eje x: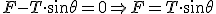

En el eje y: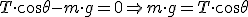

Dividiendo ambas ecuaciones, se obtiene la expresión de F en función del ángulo θ: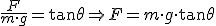

Dado que la fuerza F no es sino la fuerza de Coulomb de repulsión entre cargas 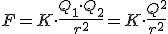, y teniendo en cuenta que, por trigonometría, la distancia r entre las cargas toma el valor 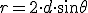, podemos encontrar fácilmente la ecuación que permite determinar la carga Q una vez conocido el ángulo θ:

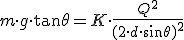
Ejemplo o ejercicio resuelto

Un electroscopio consta de dos esferas de 50 g cada una, colgadas de un cable de 50 cm de longitud. Cuando se electrizan ambas esferas positivamente con la misma carga, se observa que el ángulo formado entre cada uno de los hilos y la vertical es de 40º.

Determina la carga de las esferas.