3.5. Estructuras dinámicas no lineales
 |
| Imagen en Pixabay de TEXample.net bajo licencia Creative Common CCO |
Hasta el momento, todo lo que hemos visto han sido estructuras de datos lineales, pero en ocasiones son necesarias otro tipo de estructuras de datos jerarquizadas como pueden ser los árboles o los grafos.
El objetivo de esta sección es introducirte un poco estas estructuras con el fin de conocerlas superficialmente, requieren de experiencia y algunos conocimientos extra que impiden profundizar en su estudio.
.
A) Árboles
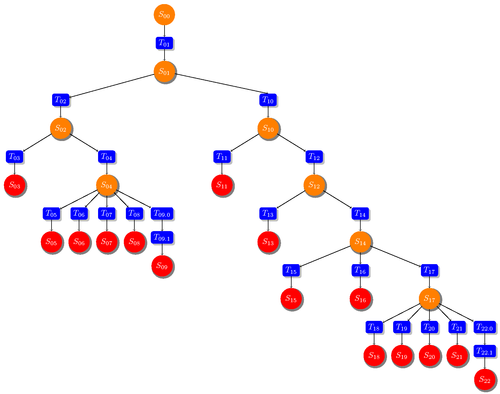
Como se ha mencionado, un árbol es una estructura de datos jerarquizada y no lineal constituida por un conjunto de elementos homogéneos, es decir del mismo tipo, que se caracterizan porque establecen una jerarquía entre los elementos que la forman. Esta relación jerárquica entre sus nodos se establece de manera que todos los nodos que componen el árbol tienen un único nodo padre, que es el nodo que le precede en la jerarquía. La única excepción es el nodo raíz, que se puede definir como aquel nodo que no tiene padre. Todos los árboles tienen una única raíz.
Cada nodo puede tener 0, 1, o más de un nodo hijo. Un nodo hijo es aquel que le sucede en la jerarquía. Si un nodo no tiene ningún hijo se le llama nodo terminal u hoja. El número de hijos que tiene un nodo es lo que denominaremos grado.
Un árbol se puede caracterizar por:
- Profundidad: máximo grado que alcanza el mismo.
- Peso: número de hojas del árbol.
Los árboles se clasifican en función del número máximo de sucesores o descendientes de un nodo, de forma que un árbol donde cada nodo tiene un máximo de dos sucesores se denomina árbol binario (son los más usados); si tiene un máximo de tres sucesores se denomina árbol ternario y así sucesivamente.
.
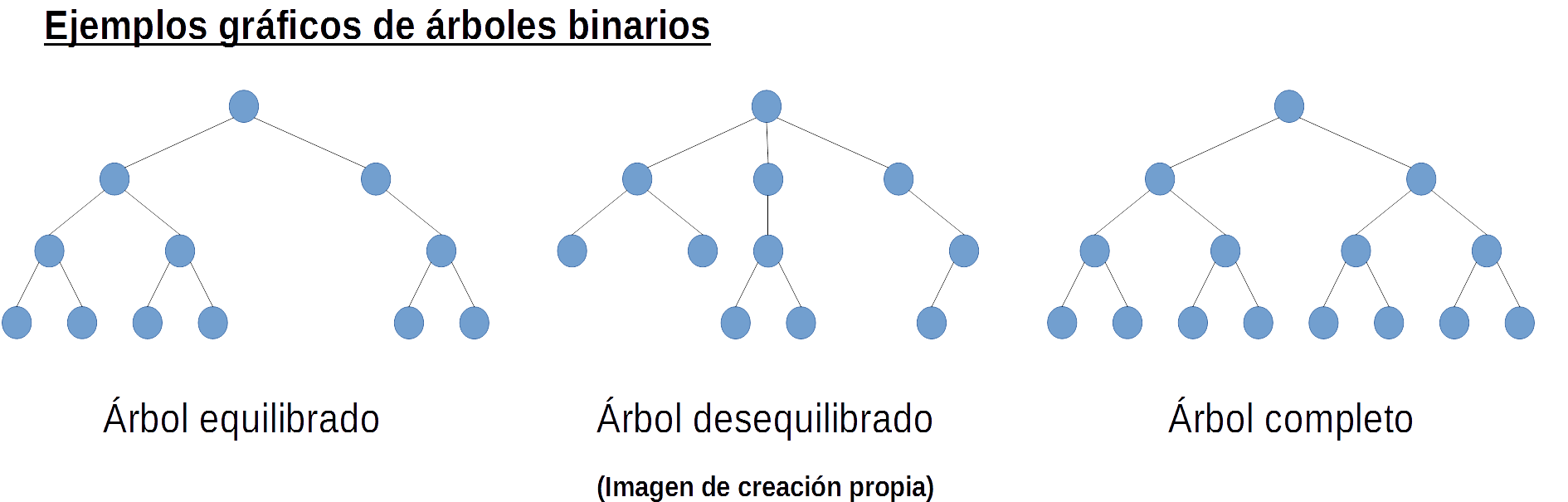
.
B) Grafos
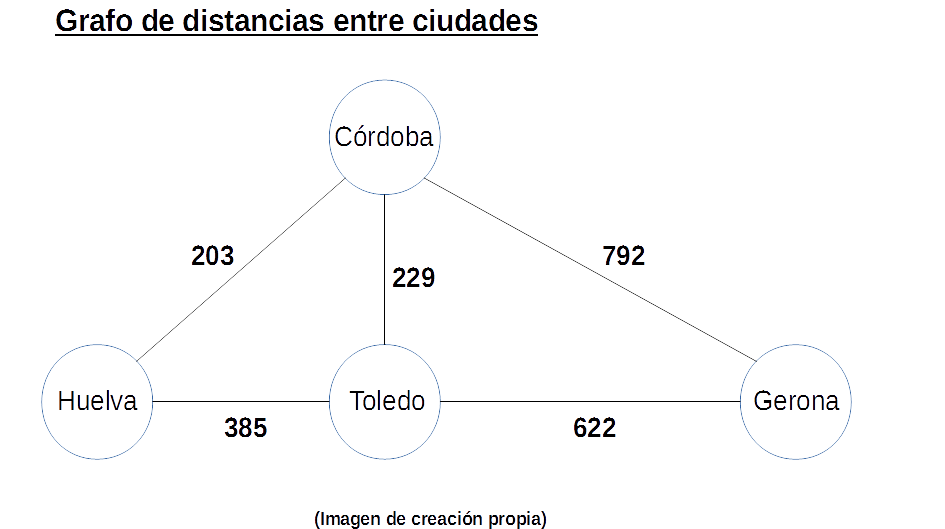
Un grafo es una estructura de datos dinámica muy similar a los árboles formado por un conjunto de nodos y otro conjunto de arcos. Cada arco agrupa a dos nodos que pueden ser el mismo. Cada arco puede tener peso, coste o distancia. Además de arcos pueden estar orientados o no estarlo. En caso de estar orientados se representan mediante una flecha, en caso contrario se representan por un segmento.
Un grafo se puede recorrer igual que un árbol, bien por profundidad o bien por anchura.
Algunos algoritmos importantes, como el de Djikstra, son desarrollados mediante grafos. Resolver por ejemplo un problema de distancias entre ciudades es típico de grafos. Aquí cada vértice sería una ciudad y cada arco una carretera entre dos ciudades.
.
Para saber más
Problema del viajante
El Problema del Agente Viajero (TSP por sus siglas en inglés) o problema del viajante, responde a la siguiente pregunta: Dada una lista de ciudades y las distancias entre cada par de ellas, ¿cuál es la ruta más corta posible que visita cada ciudad exactamente una vez y regresa a la ciudad origen? Este es un problema NP-duro dentro en la optimización combinatoria, muy importante en la investigación de operaciones y en la ciencia de la computación.
El problema fue formulado por primera vez en 1930 y es uno de los problemas de optimización más estudiados. Es usado como prueba para muchos métodos de optimización. Aunque el problema es computacionalmente complejo, una gran cantidad de heurísticas y métodos exactos son conocidos, de manera que, algunas instancias desde cien hasta miles de ciudades pueden ser resueltas.
La solución más directa puede ser, intentar todas las permutaciones (combinaciones ordenadas) y ver cuál de estas es la menor (usando una Búsqueda de fuerza bruta).
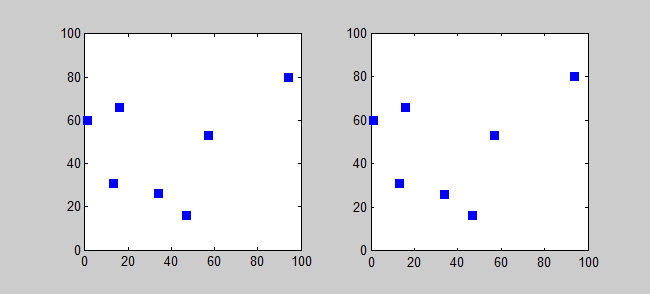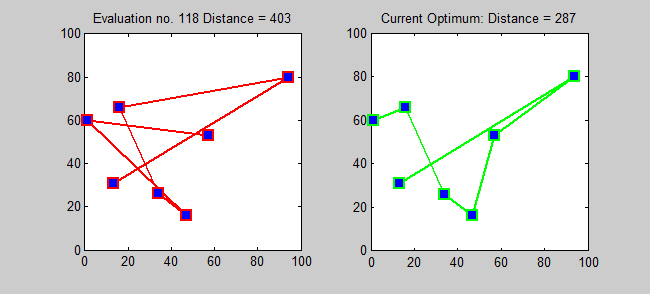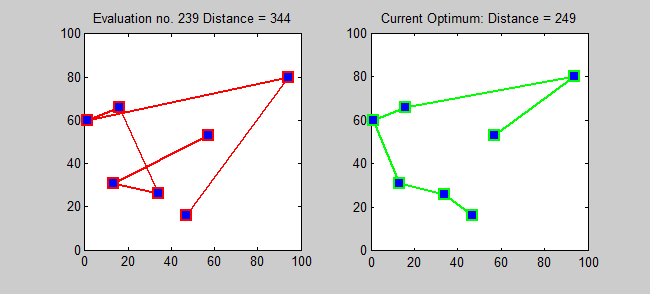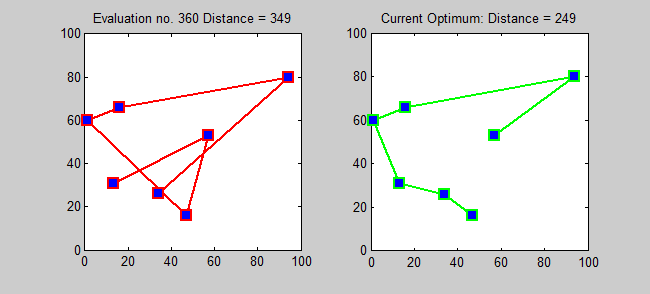
(Texto e imágenes de Wikipedia bajo licencia CCM)