1.3. Parámetros

Un logotipo
 Imagen en Flickr
de Jordan Lloyd bajo CC

Como hemos podido ver en el apartado anterior, una distribución de probabilidad de una variable aleatoria discreta no es más que una idealización de una distribución estadística donde la función de probabilidad juega el papel de las frecuencias relativas.

Por ejemplo, en la simulación del lanzamiento repetido 500 veces de dos dados, obtuvimos que la frecuencia relativa de 8 era 0.16, en tanto que dedujimos que la función de probabilidad de 8 es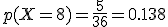

Al igual que ocurría con la distribuciones estadísticas, podemos hallar los parámetros de las distribuciones de probabilidad.

Importante

Cualquier variable aleatoria discreta 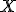, que toma valores 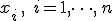y con función de probabilidad 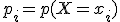, tiene asociado los siguientes parámetros:

Media o esperanza matemática: 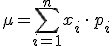. También se representa como .

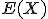Varianza: 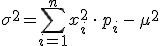 . Se representa también com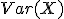o o .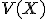

Desviación típica: 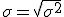. Llamada también .

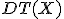Estos parámetros son similares a los de un estudio estadístico, es decir, la esperanza se corresponde con la media y es una medida de centralización de la distribución de probabilidad, en tanto que la desviación típica lo es de la dispersión.

Caso de estudio

Calcula los parámetros de la variable aleatoria asociada al experimento del lanzamiento de dos dados y sumar sus caras superiores.

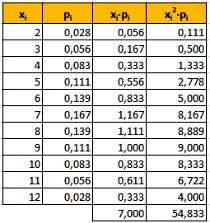
Como ayuda te aportamos una tabla con las funciones de probabilidad y algunas columnas más que te facilitarán los cálculos.

Tabla de cálculos

Imagen de elaboración propia

En este vídeo del canal de juanmemol puedes ver de forma detallada cómo se calculan todos los parámetros de una función de probabilidad asociada a una variable aleatoria discreta.