3.3 Conservación de la energía mecánica
Ejemplo o ejercicio resuelto
Veamos el movimiento de un péndulo que se separa de su posición de equilibrio.
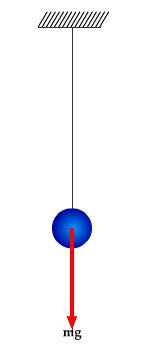
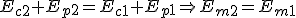
Actividad
La energía mecánica de un sistema aislado permanece constante si no existen rozamientos.
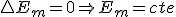
Cuando el trabajo de una fuerza sobre un sistema mantiene constante su energía mecánica, indica que dicha fuerza es conservativa.
Ejemplo o ejercicio resuelto
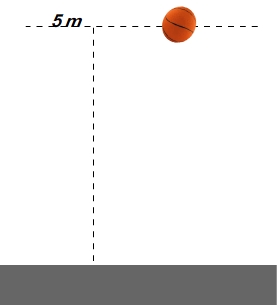 |
| Imagen de elaboración propia |
Desde una altura de 5 m se deja caer una pelota de 500 g de masa. Suponiendo que no existen rozamientos:
AV - Pregunta Verdadero-Falso
En una montaña rusa de 25 m de altura máxima, una vagoneta de masa 300 kg se mueve con una velocidad de 10 m/s alpasar por un punto situado a 20 m de altura.
Suponiendo que no existe rozamiento, indica cuáles de las siguientes afirmaciones son correctas:
Retroalimentación
Verdadero
La energía mecánica de la vagoneta es la suma de sus energías cinética y potencial:
Em = Ec + Ep = (1/2)·m·v2 + m·g·h = (1/2)·300·102 + 300·9.8·20 = 73800 J
Por lo tanto la afirmación es correcta.
Retroalimentación
Falso
Como no existen rozamientos, la energía mecánica se conserva:
ΔEm = 0 → Emi = Emf
A nivel del suelo, toda la energía mecánica estará en forma de energía cinética, puesto que la energía potencial vale cero al ser cero la altura. Por lo tanto, como la energía mecánica es de 73800 J (tal y como se ha demostrado en el apartado anterior) resulta:
Emi = Emf → 73800 = (1/2)·m·v2 + 0 → v = 22.2 m/s
que será la velocidad que lleve la vagoneta cuando pase a nivel del suelo, y no 20 m/s.
Retroalimentación
Verdadero
De nuevo aplicamos el principio de conservación de la energía mecánica:
ΔEm = 0 → Emi = Emf → 73800 = (1/2)·m·v2 + m·g·h = (1/2)·300·v2 + 300·9.8·25 → 300 = 150·v2 → v = 1.4 m/s
Luego la afirmación era verdadera.