2.2 Método de igualación
Si tenemos que pagar una compra que vale 1,10 € podemos hacerlo de distinta manera sin que tengan que devolvernos nada, entregando una moneda de euro y dos monedas de 5 céntimos, o una moneda de 50 céntimos y tres de veinte céntimos, o de otras maneras distintas. Está claro que pagamos la misma cantidad pero presentada por una combinación de monedas distintas. Cosas iguales pero expresadas de distinta manera es lo que vamos a utilizar en este método.
 |
| Fuente propia |
Pregunta de Elección Múltiple
Los pasos a seguir en el método de igualación son los siguientes:
- Despejamos en las dos ecuaciones la misma incógnita.
- Igualamos entre sí los dos valores despejados. De esa manera obtenemos una ecuación donde sólo aparece la otra incógnita.
- Se resuelve la ecuación obtenida. Así tenemos el valor de una de las incógnitas.
- Se sustituye el valor de la incógnita encontrada en cualquiera de las dos expresiones despejadas en el paso 1 y se halla el valor de la otra incógnita.
En la presentación siguiente tienes resuelto un sistema paso a paso utilizando este método.
Pregunta de Elección Múltiple
|
1. Resuelve el siguiente sistema por el método de igualación e indica la solución correcta. |
 |
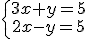| a) |   |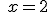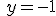
| b) |
  |
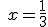| c) |   |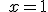
|
2. Resuelve el siguiente sistema por el método de igualación e indica la solución correcta. |
 |
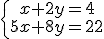| a) |
 |
| b) |
 |
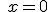| c) |  |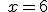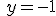
|
3. Resuelve el siguiente sistema por el método de igualación e indica la respuesta correcta. |
 |
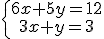| a) |
  |
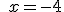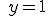| b) | |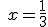
| c) |
  |
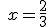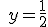