4.1 Péndulo

Imagen de burro en Wikipedia. CC	Vídeo de fgarbor906 alojado en Youtube

Imagen modificada de FJGAR (BIS) en Wikimedia. CC

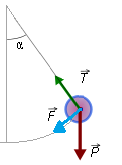
Un péndulo simple es un sistema de gran interés. Consta de una masa suspendida de un hilo, cable o varilla inextensible y de masa despreciable. En una situación estable, sobre el péndulo actúan dos fuerzas que están en equilibrio: la tensión del hilo que sostiene al objeto y el peso de este.  

Al separar el péndulo de la la posición de equilibrio, que es la vertical, un determinado ángulo , el cuerpo oscila en torno a esta posición de equilibrio, comenzando entonces un movimiento de oscilación. 

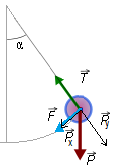
Hay por tanto una fuerza restauradora que actúa sobre el cuerpo que oscila, la puedes ver representada en la imagen de la derecha (en azul). 

Si ese ángulo es suficientemente pequeño podemos afirmar que seguirá un movimiento armónico simple.     

La fuerza restauradora será la componente tangencial del peso del cuerpo (), es decir, la parte de la fuerza peso que es tangente a la trayectoria. Tal fuerza varía su valor según la posición que ocupe el objeto oscilante.

Por otro lado, existe otra componente de la fuerza peso, la componente normal (). La misma es anulada por la tensión de la fuerza. La componente normal toma su valor máximo, o lo que es lo mismo, toma el valor del peso cuando se encuentra en la posición de equilibrio, siendo pues la otra componente nula. Ello mantiene más aún la relación con el movimiento armónico simple.

Imagen de FJGAR en Wikimedia. CC

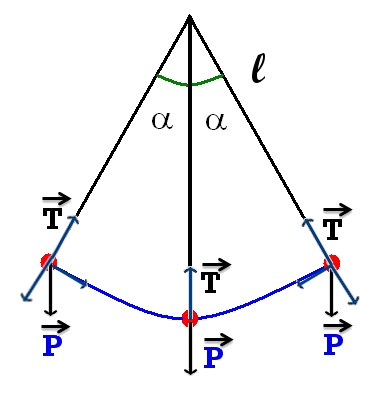
En la figura adjunta puedes ver claramente las fuerzas que intervienen en cada momento y cómo las mismas pueden descomponerse, así descubrirás cuáles se anulan y cuáles provocan el cambio de posición. Aplicando los conocimientos básicos de geometría podrás darte cuenta de que el ángulo formado por la fuerza peso y su componente normal es exactamente igual al que forma el hilo con la posición de inicio.

Por ello, se puede establecer que la componente tangencial toma la siguiente expresión:

 (el signo negativo da idea de que su sentido es hacia la posición de equilibrio).

Curiosamente, el valor de la función seno toma valores casi iguales que el propio ángulo cuando hablamos de valores muy pequeños y, por tanto, puede ser sustituido el seno por el ángulo. El valor del ángulo se puede calcular como:

Por tanto, la fuerza será:

Ya sabes que esta es la fuerza restauradora, por tanto se igualan expresiones:  y  y se llega a la siguiente expresión:  

Como  entonces: 

Y sabiendo que  obtenemos la expresión del período para el movimiento de un péndulo:

En esta última ecuación puedes observar que el período (y por tanto, la frecuencia) de un péndulo, al igual que en cualquier movimiento armónico simple, son independientes de la amplitud del movimiento. Además, para un péndulo que oscila bajo pequeños ángulos con respecto a la posición de equilibrio, el período y la frecuencia son independientes de la masa, algo que no es posible para el caso de un muelle oscilante por la acción de masa.

Esto que acabas de ver es lo que hace que los péndulos fueran empleados como instrumentos de medida del tiempo y que ambas magnitudes sólo dependen de la longitud del péndulo y de la aceleración consecuencia del campo gravitatorio terrestre.