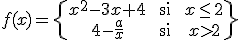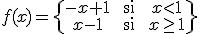4. Continuidad de una función. Discontinuidades
 |
Si recuerdas del primer tema de la unidad, dijimos que una función era continua si no tenía ninguna interrupción; si se podía dibujar de un trazo sin levantar el lápiz del papel. Esto es una visión global de la continuidad, pero cuando no hay continuidad es porque esta propiedad falla en un determinado lugar. ¿Y qué será lo que falla?
Ha llegado el momento de juntar límite y continuidad y de ver la continuidad de una función pero sin necesidad ya de tener que ver la gráfica por delante.
En este video puedes apreciar la idea de función continua. Como hemos indicado anteriormente, simplemente diremos que es continua si podemos dibujarla sin levantar el lápiz del papel. En este video puedes visualizar esta explicación.
Gráficamente, es muy sencillo determinar si una función es continua, ahora veremos cómo determinar si una función dada analíticamente es continua.
Importante
Teniendo en cuenta lo que acabamos de ver, una función es continua en x = a si:
- Existe f(a).
- Los dos límites laterales existen, son números reales y coinciden.
- El valor del límite coincide con el de la imagen.
Esas tres propiedades se resumen en: 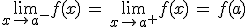
En general, todas las funciones elementales, las que has visto en el tema anterior, son continuas en sus respectivos dominios de definición.
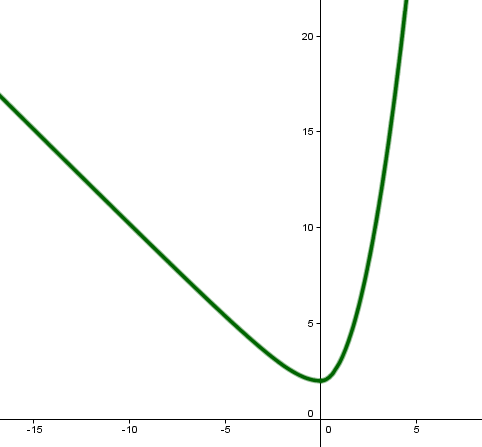 Veamos un caso concreto del estudio de una función definida a trozos y analicemos la continuidad de la función
Veamos un caso concreto del estudio de una función definida a trozos y analicemos la continuidad de la función

La función para x< 0 es continua ya que estamos ante una raiz cuadrada de un radicando siempre positivo (x2 + 4 siempre es positivo) por lo que siempre existe el resultado de dicha raiz. Si x>0 nos encontramos antes un polinomio, por lo que es continua en todo el intervalo. Tan solo debemos comprobar si la función es continua en 0
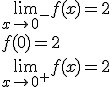
Por lo tanto la función es continua en todos los números reales.
Caso de estudio
Estudia la continuidad de la función
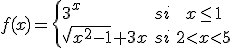
Ejemplo o ejercicio resuelto
 |
En este ejercicio, vamos a ver cómo estudiar la continuidad de una función a trozos sin necesidad de ver su representación gráfica. ¿Recuerdas el ejemplo de los sueldos de los camareros de la caseta que vimos en el apartado 2?
Teníamos que la función que le daba a Nacho el dinero a pagar a cada camarero de la caseta según las horas que trabajaba era:
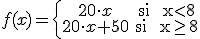
¿Será esa una función continua?
AV - Reflexión
La función f(t) que mostramos a continuación muestra el beneficio de la empresa EXRED (en cientos de miles de euros) a lo largo de los diez primeros años tras su fundación. La función donde t expresa el tiempo en años es:
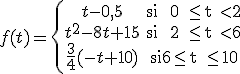
¿Es continuo el crecimiento de los beneficios de la empresa?
Ejemplo o ejercicio resuelto
 SEPTIEMBRE 2011. ANDALUCÍA
SEPTIEMBRE 2011. ANDALUCÍA
Sea la función real de variable real:
(a) (1’5 puntos) Halle el valor de a para que dicha función sea continua y estudie la derivabilidad de f para ese valor de a.
(b) (1 punto) Para a = 1, ¿existe alguna asíntota vertical de esa función? ¿y horizontal? Razone las respuestas y calcule, en caso afirmativo, dichas asíntotas.
Nota: Sólo no podemos realizar el estudio sobre la derivabilidad del apartado (a). Para ello tendrás que esperar a próximos temas.
Ejemplo o ejercicio resuelto
 JUNIO 2009. ANDALUCÍA
JUNIO 2009. ANDALUCÍA
Sea la función real de variable real:
a) (1 punto) Represente gráficamente la función.
b) (1 punto) Estudie la continuidad de la función.
c) (1 punto) Estudie la derivabilidad de la función.
Nota: El apartado c) requiere de lo que se impartirá en los próximos temas. Sin embargo, los apartados a) y b) sí puedes afrontarlos con lo aprendido hasta ahora.
Para saber más
En este vídeo te mostramos cómo calcular una incógnita o dos dentro de una función a partir de la idea de que la función tiene que ser continua. Este ejercicio es de los clásicos de selectividad, así que si estás pensando en ello, debes verlo y entenderlo:
Si quieres hacer algunos ejercicios de este estilo, en esta presentación encontrarás varios.
Actividad
Una discontinuidad se dice evitable en x= a si existe el límite de la función en el punto y es finito, pero no coincide con el valor f(a) o no existe dicho valor.
La discontinuidad se llama de tipo evitable, ya que podemos evitar la discontinuidad si definimos 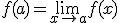
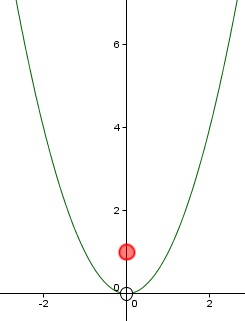
Veamos un caso concreto, la función definida como
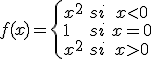
Esta función, para el valor x = 0, verifica que f(0) = 1 tal y como hemos definido la función, sin embargo, 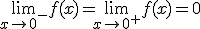 . Por lo tanto , la función presenta una discontinuidad evitable tal y como podemos ver en su representación, ya que si definimos f(0) = 0, la función sería continua.
. Por lo tanto , la función presenta una discontinuidad evitable tal y como podemos ver en su representación, ya que si definimos f(0) = 0, la función sería continua.
Actividad
Una función presenta una discontinuidad en x= a de salto o de primera especie si existen los límites laterales y son distintos o al menos uno de ellos es infinito.
Se dirá que la discontinuidad es de salto finito si los límites laterales son finitos y de salto infinito si al menos uno de ellos es infinito.
 |
|
Imagen en Wikimedia Commons
creada por Omegatron. Dominio Público |
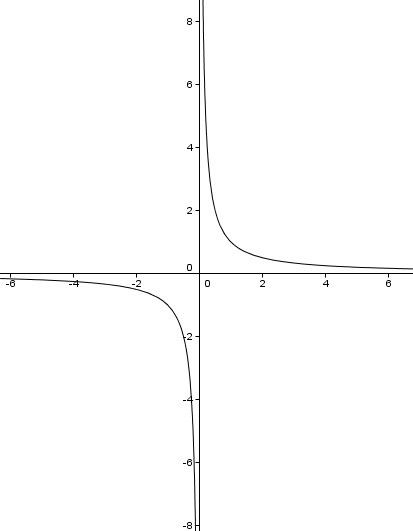
Un ejemplo muy visual de función con una discuntinuidad de primera especie en x= 0 y en particular de salto infinito es 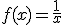 , ya que al estudiar los límites laterales en el punto x= 0 obtenemos
, ya que al estudiar los límites laterales en el punto x= 0 obtenemos 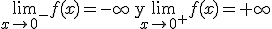
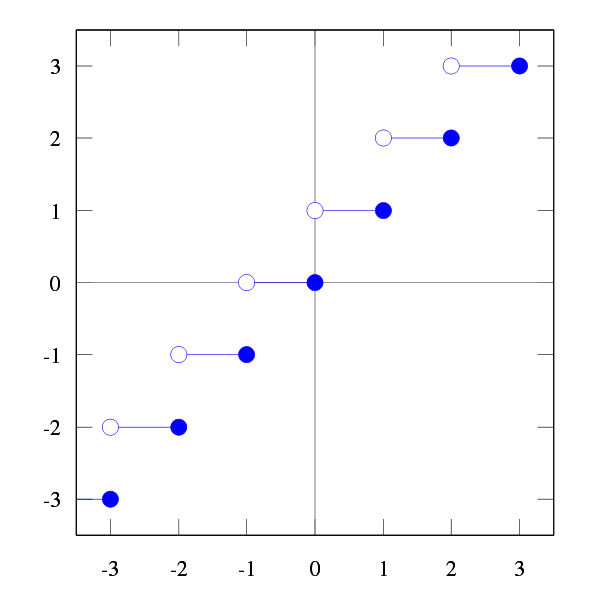
Si tomamos la función f(x) = Ent(x), es decir la parte de entera de un número detectamos que dicha función tiene una discontinuidad de 1º especie, de salto finito en los números enteros. Estudiemos, por ejemplo, la discontinuidad en x= 1
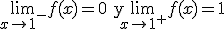
Actividad
Una función f(x) presenta una discontinuidad de segunda especie en el punto x= a si no existen uno de los límites laterales
|
Imagen en Wikimedia Commons. Dominio Público
|
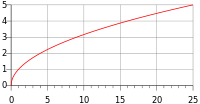
Algunos funciones no están definidas para ciertos valores, de hecho, ya vimos que la función solo existe para los puntos de su dominio.
Si analizamos la función 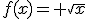 , el dominio de esta función son los reales positivos incluido el cero. Al estudiar las discontinuidades de dicha función, podemos observar que el límite por la izquierda en x= 0 no existe, por lo que la función presenta una discontinuidad de segunda especie en x =0 . Al calcular el límite por la derecha, observamos que
, el dominio de esta función son los reales positivos incluido el cero. Al estudiar las discontinuidades de dicha función, podemos observar que el límite por la izquierda en x= 0 no existe, por lo que la función presenta una discontinuidad de segunda especie en x =0 . Al calcular el límite por la derecha, observamos que 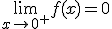
Caso de estudio
Estudia la continuidad de la siguiente función f(x) e indica, si existe, su tipo de discontinuidad.
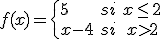
Caso de estudio
Estudia las discontinuidades y sus tipos de la función 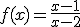
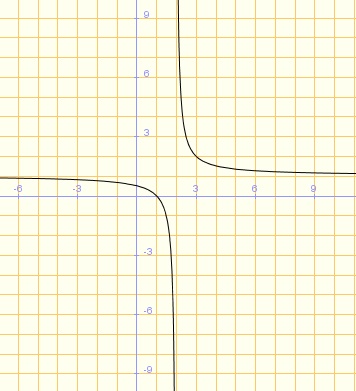
Pregunta de Elección Múltiple
En el siguiente documento creado por Alberto Adones puedes apreciar un par de actividades relacionadas con las discontinuidades