3.1. Indeterminaciones
 |
En el apartado anterior, hemos dicho que para calcular el límite de una función en un punto basta con sustituir el valor de x en la función y que si las operaciones se pueden hacer, el resultado obtenido es el del límite. Pero, ¿cuándo no se pueden hacer las operaciones? Pues por ejemplo, cuando estamos haciendo una raíz cuadrada y dentro nos sale un número negativo, o cuando estamos haciendo una división y tenemos que dividir entre cero. Pruébalo, coge una calculadora y divide cualquier número entre 0, ¿qué ocurre? ¿qué te muestra?
Que nada de nada, que no existe, pero claro si lo piensas fríamente es así. ¿Cómo vas a repartir 8 caramelos entre 0 niños? ¿Cómo vas a hacer el reparto si no tienes a quien dárselos?
En este último caso, la operación directa no se puede hacer pero si nos vamos aproximando sí que obtenemos algún resultado. Estos casos son los que se llaman indeterminaciones y en este apartado vamos a ver cómo se resuelven algunos de los tipos más característicos.
Empezamos con este, con el dividir un número entre 0 que en general se conoce o se expresa por indeterminación 
Ejemplo o ejercicio resuelto
 |
La freidora de la caseta de feria tiene una capacidad de 12 litros. Si la llenamos con botellas de litro necesitamos 12, si la llenamos con botellas de medio litro necesitamos 24. Si las botellas son de 20 cl, o sea, 0,2 litros, necesitamos 60 y así, a medida que la capacidad de la botella es menor, más botellas hacen falta.
Si llamamos x, a la capacidad de la botella de aceite (en litros), el número de botellas necesarias vendrá dada por la función:
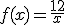
¿Cuántas botellas hacen falta si la capacidad de cada una es muy pero que muy pequeña?
Importante
Y todavía más raro, ¿puede pasar que también el numerador sea cero? Si un número entre 0 es infinito, ¿0 entre 0 qué será? ¿0? ¿Infinito? ¿1?
Pues esto de cero partido cero sí que es una verdadera indeterminación porque puede ser cualquier cosa. Puede ser 0, puede ser ∞, puede ser 1, puede ser 14, puede ser...
Cuando ocurre esto, tenemos que conseguir simplificar la fracción y para ello hemos de conseguir factorizar los polinomios del numerador y denominador.
Una vez hecho esto y simplificada la expresión, la indeterminación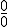 
habrá desaparecido y se podrá calcular el límite.
Te enseñamos cómo hacerlo en los siguientes vídeos. En el primero sale 1,5 y en el segundo infinito, pues al resolverlo, vamos a parar ahora al caso k/0:
|
Límite de una función racional
Vídeo alojado en Youtube
|
Límite de una función en punto (indeterminación 0/0)
Vídeo alojado en Youtube
|
Rellenar huecos
Calcula el valor de los siguientes límites. En caso de que alguno sea infinito, escribe el signo y a continuación sin dejar espacio en blanco I. Por ejemplo, si quieres escribir -∞, has de teclear "-I"
Si el resultado sale una fracción, utiliza la barra inclinada para separar. Por ejemplo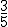 
escríbelo así: 3/5
Para saber más
Esto se puede complicar todo lo que se quiera. Según cómo sea la función, el límite es más fácil o más complicado de calcular.
En el siguiente vídeo, se muestra cómo se resuelve una indeterminación 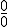cuando en el numerador o denominador de la fracción hay algún término dentro de una raíz cuadrada y otra cantidad sumando o restando fuera.
 |
¡Japón!, ¡"miá" que está lejos Japón!
No sé la edad que tienes pero lo mismo recuerdas una canción que comenzaba así del grupo sevillano "No me pises que llevo chanclas". Pues como está tan lejos, podemos decir que allí está el infinito.
Bueno, bromas aparte, vamos a ver en este apartado otro tipo indeterminación que ocurre ahora cuando se toma límite cuando x tiende a infinito.
En el ámbito de las Ciencias Sociales, es muy habitual que haya que calcular el límite de una función racional cuando x tiende a infinito. Basta que queramos saber el comportamiento de una población, del dinero invertido en un banco, de la evolución de un negocio, de la evolución de un mercado de valores, ...., a largo plazo. Muchas de estas funciones responden a funciones racionales, o sea, a dividir dos polinomios, y como ya sabes del punto 2, el resultado del límite cuando x tiende a infinito de un polinomio es infinito. Luego en este caso tendríamos que dividir infinito entre infinito. Tenemos ahora entonces la indeterminación ∞ / ∞.
Seguramente has pensado que eso es 1, si se dividen dos cantidades iguales el resultado es 1. Pero eh ahí el porqué esto es una indeterminación porque no sabemos si esos infinitos son iguales o uno es mucho más grande que otro. Es decir, hay que averiguar que relación hay entre esos infinitos, y al final, el resultado puede ser efectivamente uno, pero también puede ser cero, infinito o cualquier número real.
Ejemplo o ejercicio resuelto
 |
El número de individuos, en millones, de una población viene expresada por la función:
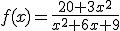
donde x indica el tiempo que va transcurriendo desde este momento. ¿Qué ocurre con esta población a largo plazo? ¿A qué tiende este pueblo, a estabilizarse, a desaparecer o a crecer indefinidamente?
 |
Vemos otro ejemplo:
La siguiente función muestra el número de clientes dispuestos a contratar un producto financiero desde el momento en que se lanza la oferta y sin ningún tipo de publicidad posterior ( x en meses):
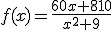
¿Cuántos clientes contratarán ese producto si el tiempo se hace infinitamente grande?
Importante
Para resolver la indeterminación ∞ / ∞, nos quedamos con los términos de mayor grado del numerador y del denominador, simplificamos y volvemos a tomar límite.
- Si el grado del numerador es mayor que el del denominador, el resultado del límite será ±∞.
- Si los grado son iguales, el resultado será el número que resulte de dividir los dos coeficientes.
- Si el grado del denominador es mayor, el resultado será 0.
AV - Actividad de Espacios en Blanco
Para saber más
En estos dos últimos apartados del tema hemos visto tres tipos de indeterminaciones, pero hay más. Si quieres saber cuáles son y cómo se resuelven sigue los enlaces que te proponemos en las siguientes páginas:
Al calcular el término n de la ecuación, nos encontramos con límites del tipo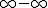 
. Veamos varios límites de este tipo y cómo se resuelven.