3.1 Formulación vectorial
Si lees atentamente el enunciado de la ley, podrás intuir que la expresión matemática anterior solo representa parte de la situación. Implícitamente, en la misma se atisba que debe tener cierta importancia la dirección, ya que se indica que la distancia es del centro al centro de cada cuerpo.
Por otro lado ya sabes, porque así lo estudiaste en la unidad de Dinámica, que si observas los efectos que produce una interacción notarás que son distintos según sea la intensidad de la misma, la dirección en que se produce, su sentido y el punto donde se aplica. Por esto, una interacción debe representarse mediante una magnitud vectorial.
Así, la fuerza será una magnitud vectorial, por lo que su definición correcta será:
\[\overrightarrow{F}=-G\cdot \frac{M\cdot m}{r^2}\cdot \overrightarrow{u_r}\]
donde ![]() representa un vector unitario en la dirección de la recta que une los centros de ambos cuerpos.
representa un vector unitario en la dirección de la recta que une los centros de ambos cuerpos.
Se ha determinado, para llegar a esta expresión, que el origen del sistema de referencia es la masa M, generalmente la masa mayor. Con esta ecuación se determina la fuerza que siente el cuerpo m debido a la atracción que ejerce M.
El vector de posición de la masa m () es el vector que va desde M hasta m. El vector unitario
![]() es un vector con dirección y sentido del vector de posición, de módulo igual a uno.
es un vector con dirección y sentido del vector de posición, de módulo igual a uno.
- El módulo de la fuerza gravitatoria queda expresado por la ley de gravitación universal.
- La dirección será la de la recta que los une, es decir, la dirección del vector de posición que coincide con la dirección de
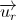 .
. - Esta fuerza gravitatoria es (que realiza M sobre m) es una fuerza de atracción, por lo que el sentido de la fuerza gravitatoria irá de forma que m se dirige hacia M, es decir, sentido contrario a
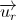 , por ello se incluye el signo menos en la expresión vectorial.
, por ello se incluye el signo menos en la expresión vectorial.
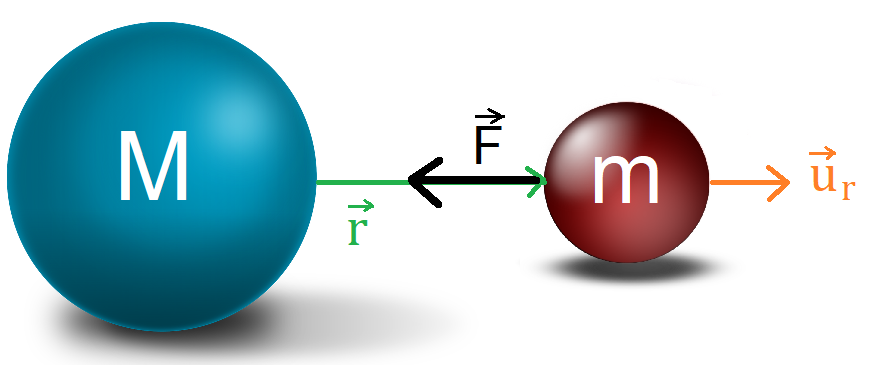 |
| Imagen de CharoSaa en Wikimedia Commons. CC |