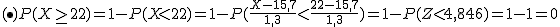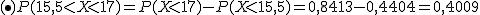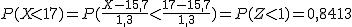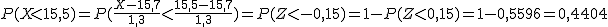4. Tipificación de la distribución normal
El apartado anterior lo hemos dedicado completamente al estudio de la distribución normal estándar, la N(0,1). Pero dirás con toda la razón: "todo en la vida no es estándar". Es decir, ¿si tenemos una distribución N(μ,σ), distinta de la estándar y queremos calcular probabilidades con ella, cómo lo hacemos?
Tranquilo, ese es precisamente el objetivo de este apartado.
A continuación, veremos cómo es posible convertir cualquier N(μ,σ) en una N(0,1) (normal estándar) y como de ésta última tenemos la tabla y las propiedades que hemos visto en el apartado anterior. Entonces, ya será posible calcular probabilidades en cualquier N(μ,σ), bien usando las propiedades y la tabla o bien echando mano de las propiedades y los applets.
Seguro que has visto muebles modulares, con medidas estándar, que se colocan y apilan la mar de bien. Pero seguro, que tambien habrás visto alguna vez un rincón de tu casa o una cocina en la que los muebles con medida estándar no pueden utilizarse. En estos casos difíciles, habrás comprobado cómo los carpinteros hacen un trabajo magnífico, para que al final todo encaje a la perfección. Pues ésto, más o menos, salvando las distancias, es lo que intentaremos hacer nosotros con las distribuciones normales: estandarizarlas.
En el lenguaje matemático, el término (la palabra) utilizado para denominar a este proceso es: tipificar
Importante
Observemos las siguientes propiedades de una variable aleatoria:
(1) Si tenemos una variable aleatoria y le restamos un número, la media (μ) de la variable disminuye tambien ese número.
(2) Si tenemos una variable aleatoria y la dividimos por un número, la desviación típica (σ) de la variable tambien queda dividida por ese número.
Teniendo en cuenta (1) y (2) podemos afirmar lo siguiente:
Para transformar, X, una variable aleatoria normal, N(μ,σ), en Z, variable normal estándar, N(0,1), primero se le resta μ a X y luego se divide entre σ:
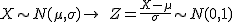
A este proceso se le llama tipificar la variable aleatoria X.
Ejemplo o ejercicio resuelto
Vamos a aplicar la tipificación de variables normales a un problema real de consumo.
 |
| Imagen de Diego López con licencia by-sa-2.0-deed |
¡Delicioso problema, si eres amante del marisco!
El precio del kilogramo de gambas frescas en el mercado de abastos de Huelva sigue una distribución normal de media: 16,5 € y desviación típica: 2 €.
Suponiendo que la distribución de precios del kilogramo de gambas es una distribución normal, responde a las siguientes cuestiones:
(a) ¿Cuál es la probabilidad de que un kilogramo de gambas nos cueste menos de 15 €?
(b) ¿Y la probabilidad de que nos cueste entre 15 y 17 €?
AV - Actividad de Espacios en Blanco
 |
Es tu turno. Te toca responder a las preguntas que se plantean sobre el siguiente problema.
Chicos y chicas
Las edades de un pandilla de jóvenes sigue una distribución normal de media 15,7 años y desviación típica 1,3 años.
Completa todas las respuestas y, posteriormente, pulsa el botón Comprobar.
Objetivos
Si quieres consolidar la tipificación de variables, aquí tienes más actividades.
(1) Si X ~ N(2;0,8), calcula P(-2<X<2)
(2) Si X ~ N(-0,5;1,5), calcula P(-2<X<2)
(3) Si X ~ N(4,7;1,2), calcula P(X<2)
(4) Si X ~ N(-3;1,3), calcula P(X>-5)
Nota: Puedes comprobar los resultados en el apartado Campana sobre campana, donde calculamos exactamente las mismas, con ayuda de un applet de Geogebra. En esta ocasión, el objetivo es que realices los cálculos con bolígrafo y papel, haciendo uso de la tipificación de variables y de las propiedades de la distribución normal.
Pre-conocimiento
|
Distribución Normal
Vídeo alojado en Youtube
|
La normal aplicada a un proyecto de construcción.
Vamos a terminar el apartado con un vídeo muy simpático pero, al mismo tiempo, tremendamente realista.
En el mismo se muestra una más de las múltiples aplicaciones y presencias que tiene la distribución normal en nuestras vidas.
Espero que sirva para sacarte una sonrisa y te ayude a afrontar con buena predisposición el resto del tema.
¡Ánimo que ya queda poco!
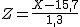 que sigue una distribución N(0,1).
que sigue una distribución N(0,1).