2. Inecuaciones con dos incógnitas
Importante
Resolver una inecuación con dos incógnitas consiste en hallar todos los puntos del plano que verifican dicha inecuación. Para ello, procederemos de la siguiente forma:
1º) Convertimos la inecuación en ecuación.
2º) Podemos despejar la variable y y representar la recta obtenida mediante una tabla de valores. Dicha recta divide al plano en dos zonas (semiplanos).
3º) Elegimos un punto de cualquiera de estos semiplanos y sustituimos en la inecuación de partida.
4º) Si el punto verifica la inecuación, el semiplano solución será la zona donde se encuentra dicho punto. En caso contrario,será la otra.
5º) Los puntos sobre la recta forman parte de la solución siempre y cuando en la inecuación de partida tengamos los símbolos ![]() o
o ![]()
En la siguiente escena, basada en una creada con Geogebra por José Álvarez y modificada, puedes ver el comportamiento de un punto sobre una recta y las posiciones relativas de dicho punto respecto a la recta.
Ejemplo:
Resuelve gráficamente la inecuación 2x+y≥-3
Si vamos a proceder a realizarlo manualmente, "sobre el papel", convertimos la inecuación 2x+y≥-3 en ecuación 2x+y=-3
Despejamos la variable y y representamos la recta y=-3-2x.
Buscamos la zona correspondiente a la solución probando con un punto.
El más fácil es el (0,0), sustituimos en la inecuación, resultando: 2·0+0=2 ≥ -3
Por tanto la zona es "la que contiene al (0,0)".
Puedes utiiizar el siguiente enlace para trabajar la representación gráfica directamente con Desmos.
La solución gráfica sería:
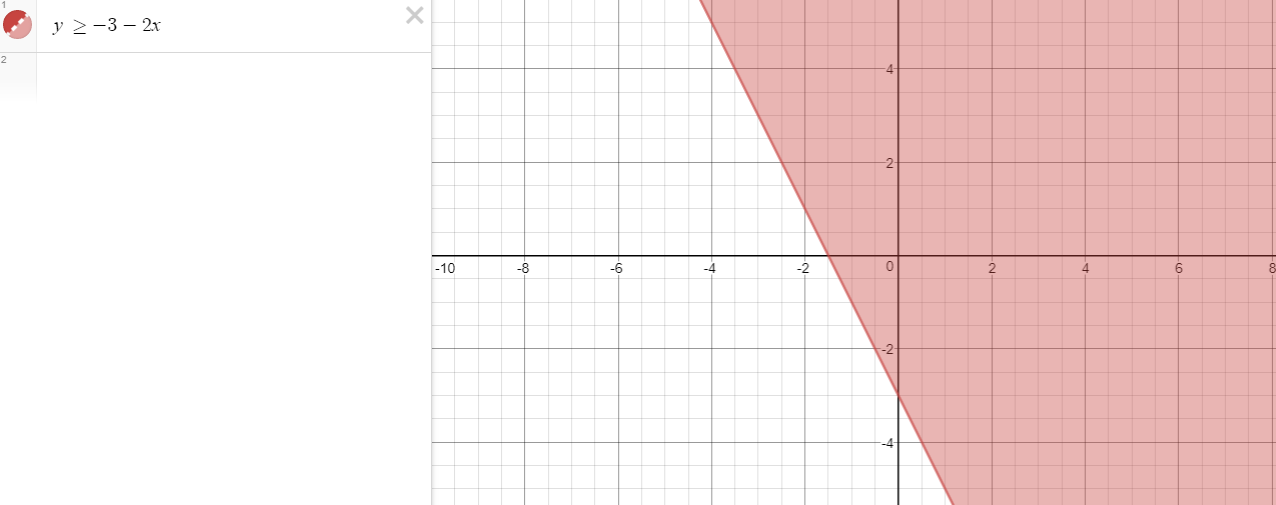
Observa que en este caso también se incluye la propia recta, ya que los puntos sobre la recta son los que verfican la igualdad 2x+y=-3 y por tanto, cumplen con la condición de la inecuación. Cuando la desigualdad sea estricta, es decir, "<" o ">", los puntos sobre la recta no serán solución y dibujaremos ésta con trazo más fino o discontinuo.
Ejemplo o ejercicio resuelto
Resuelve las siguientes inecuaciones:
a) 3x+4≥y
b) x-y<5
c) -2x+3y>0