1. ¿Debemos usar siempre el mismo tipo de recta de regresión?
¿Quieres saber más de estadística?
Te presentamos en esta sección la posibilidad de ampliar y profundizar en tus conocimientos de Estadística. Los conceptos y métodos que te mostramos aquí no tienen carácter evaluable. No pertenecen a los contenidos mínimos exigibles. Si así lo deseas, puedes interesarte por ellos ahora o en cualquier otro momento de tu proceso de aprendizaje. Tienen un carácter voluntario y tú decides el momento de adquirir dicho conocimiento. No obstante, puede resultar interesante tener un primer acercamiento a esta información que se te brinda.
1.- Situaciones raras provocadas por los puntos atípicos y extremos
Hemos visto que el método de mínimos cuadrados es una técnica habitualmente utilizada para ajustar una línea recta a un conjunto de datos con el objetivo de modelar la relación entre dos variables. Aunque es ampliamente aplicado y tiene sus ventajas, también presenta ciertos inconvenientes que debemos considerar:
Sensibilidad a valores atípicos: Los valores atípicos pueden ejercer una influencia desproporcionada en el ajuste de la recta de mínimos cuadrados. Esto significa que incluso unos pocos valores extremos pueden afectar significativamente a la pendiente y a la posición de la recta ajustada.
Influencia de puntos extremos: Los puntos extremos o valores extremos pueden tener un impacto desproporcionado en el ajuste de la recta de mínimos cuadrados, especialmente si hay pocos datos disponibles. Esto puede llevar a una interpretación errónea de la relación entre las variables o a la identificación de tendencias que no son representativas del conjunto de datos en su conjunto.
Limitaciones en la forma funcional: La recta de mínimos cuadrados asume una relación lineal entre las variables, lo que puede no ser apropiado para todos los conjuntos de datos. En presencia de relaciones no lineales, este método puede producir estimaciones inadecuadas o poco precisas. Este hecho lo hemos paliado ajustando la nube de puntos a otros modelos (potencial, logarítmico, exponencial, etc.)
En resumen, aunque el método de mínimos cuadrados es ampliamente utilizado y tiene sus ventajas, es importante ser consciente de sus limitaciones y considerar alternativas cuando sea necesario, especialmente en presencia de valores atípicos, violaciones de supuestos o relaciones no lineales entre las variables.
Ejemplo 1.- Puntos atípicos. Ajustar un modelo lineal a la distribución bidimensional dada por la siguiente tabla:
| X | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 21 |
| Y | 9 | 11 | 13 | 13 | 15 | 14 | 16 | 1 | 16 | 14 | 19 | 2 |
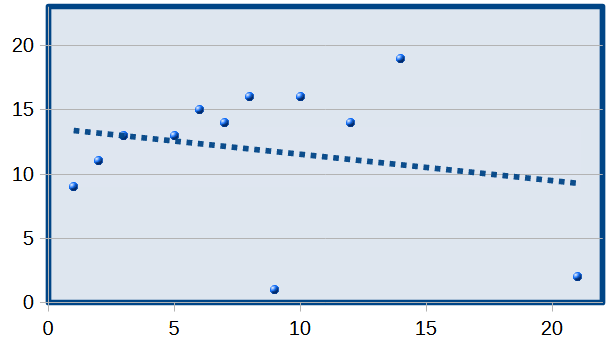
En algunos casos, la recta de regresión se ajusta muy mal a la nube de puntos, a pesar de que a simple vista los puntos parecen indicar una correlación lineal. La variable Y toma dos valores, 1 y 2, que están muy alejados del resto. En la Fig.1, se ha representado la recta de regresión de Y sobre X y se aprecia su mal ajuste a la nube de puntos.
Ejemplo 2.- Puntos extremos. Ajustar un modelo lineal a la distribución bidimensional dada por la siguiente tabla:
| X | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 15 |
| Y | 6 | 11 | 13 | 13 | 15 | 14 | 16 | 15 | 16 | 14 | 6 | 4 |
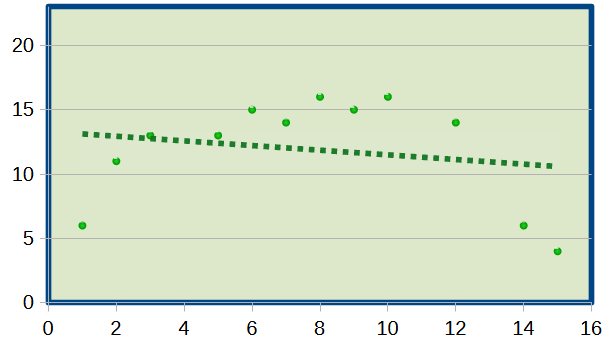
En este otro caso vemos cómo influyen los puntos extremos (14,6) y (15,4). Observamos en la Fig. 2, que lejos de continuar la recta con una tendencia creciente, como la que se seguía hasta llegar a estos dos puntos extremos, se cambia bruscamente la monotonía de la recta. De este modo se consigue un mal ajuste con la recta de regresión. La influencia de estos puntos extremos ha procurado al final que la recta se desvíe notablemente de la inercia que mantenía. (Ver Fig. 2).
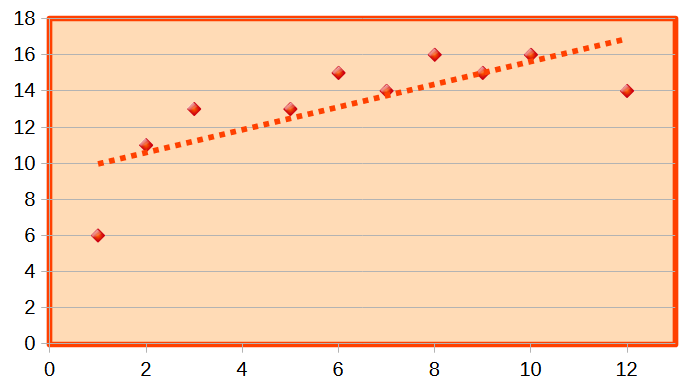
Veamos ahora qué pasaría si eliminásemos estos dos puntos extremos, notablemente tendenciosos, y que han condicionado tan fuertemente la pendiente de la recta de regresión. ¿Crees que cambiaría mucho la gráfica? En efecto, mira en la Fig. 3, el resultado que se conseguiría. Sin embargo, si hubiéramos cambiado algunos puntos centrales de la distribución, este hecho no hubiera afectado tanto a la posición final de la recta de regresión.
Pues bien, en el siguiente apartado mostraremos alguna técnica estadística como remedio a estas situaciones. Te adelantamos que la alternativa a la Recta de Regresión se llamará Recta de Tukey, en honor a su descubridor, John W. Tukey (1915-200).
2.- Recta de Tukey
El procedimiento de Mínimos Cuadrados es un procedimiento clásico muy empleado, que permite estudiar la relación lineal entre variables, mediante una ecuación lineal o recta de regresión. El método de Mínimos Cuadrados sirve para ajustar una recta a una serie de puntos que guarden una relación lineal. El criterio de este método es el siguiente: La recta se ha de construir de tal manera que la suma de los cuadrados de las desviaciones verticales de todos los puntos respecto a la recta sea mínima. Sin embargo, este procedimiento es poco resistente, ya que, al tener en cuenta todas las puntuaciones (observar que al utilizar las Medias de X y de Y en las fórmulas, usamos todos los valores), puede resultar alterado fácilmente por la existencia de unas pocas puntuaciones atípicas.
El Método de la Recta de Tukey.
El método denominado "Línea de Tukey", también denominado "método de la línea resistente de tres grupos" es un procedimiento resistente para observar la relación lineal entre dos variables. Para ello, emplea un estadístico resistente como la Mediana que, como ya ha sabemos es un estadístico que se halla poco afectado por las puntuaciones extremas, ya que no tiene en cuenta todas la puntuaciones, sino solamente las centrales, a diferencia de la Media Aritmética. Por ello, el método de la Línea de Tukey es asimismo resistente. Describimos ahora los pasos a seguir:
- Ordenar los n pares de valores en función de la variable X, en orden ascendente.
- Dividir las n observaciones ordenadas de X en tres grupos, con sus respectivos valores en Y, cada uno de los grupos con, aproximadamente un tercio de las observaciones. De este modo, se obtendrá un grupo inferior (el primer tercio de puntuaciones de X), un grupo medio (el segundo tercio de puntuaciones) y un grupo superior (con las n/3 puntuaciones mayores en X).
- Sin embargo, este paso puede plantear algunos problemas. Concretamente, nos referiremos a la existencia de una restricción que señala que dos puntuaciones de X con el mismo valor, es decir, los empates, deben estar en el mismo grupo. Por ejemplo, en el conjunto ordenado de puntuaciones de la variable X: 3,3,3,4,4,4,4,5,5; habrá tres grupos, el primero formado por los tres primeros, un segundo formado por los cuatro siguientes (y no sólo por los tres siguientes, para no separar las puntuaciones iguales), mientras que el grupo superior estará formado por las dos últimas puntuaciones.
- Averiguar la Mediana de la variable X en el primer grupo (que denotaremos MdX1), así como la de Y también en el primer grupo (MdY1).
- Averiguar la Mediana de la variable X (MdX2), así como también la de Y (MdY2), en el segundo grupo.
- Averiguar la Mediana de la variable X (MdX3), así como también la de Y (MdY3), en el tercer grupo.
- Si la recta viene dada por su ecuación punto-pendiente del modo $y=b·(x-x_G)+y_G$, sabemos que esta recta tiene como pendiente:
$p={\large{\frac{MdY_3-MdY_1}{MdX_3-MdX_1}}}$
y además ha de pasar por el punto G, llamado baricentro de la distribución, donde:
$G=\left({\large{\frac{\text{MdX}_1+\text{MdX}_2+\text{MdX}_3}{3}}},{\large{\frac{\text{MdY}_1+\text{MdY}_2+\text{MdY}_3}{3}}}\right)$. - Si la ecuación de esta recta viene dada por $y=a+px$, obtenemos a partir de la ecuación anterior, los valores de $a$ (la ordenada en el origen) y $p$ (la pendiente). Los respectivos cálculos son:
$p={\large{\frac{MdY_3-MdY_1}{MdX_3-MdX_1}}}$;
$a=\sum _{i=1}^3 {\large{\frac{\text{MdY}_i-b\cdot \text{MdX}_i}{3}}}={\large{\frac{\text{MdY}_1-b\cdot \text{MdX}_1}{3}}}+{\large{\frac{\text{MdY}_2-b\cdot \text{MdX}_2}{3}}}+{\large{\frac{\text{MdY}_3-b\cdot \text{MdX}_3}{3}}}$
3. Recta de Tukey: Ejercicios de aplicación
Ejemplo 1.- Sea la variable bidimensional dada por la siguiente tabla.
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 5 | 6 | 8 | 11 | 1 | 13 | 14 | 14 | 17 |
i) Halla la recta de Tukey.
ii) Halla la recta de regresión de Y sobre X.
iii) Representa la nube de puntos y las dos rectas obtenidas.
Solución.-
Apartado i) Recta de Tukey
a) Formamos los grupos para las abscisas X:
Gx1={1,2,3}; Gx2={4,5,6}; Gx3={7,8,9}. Sus respectivas medianas son:
$Mdx_1=2;Mdx_2=5;Mdx_3=8$
b) Formamos los grupos para las ordenadas Y:
Gy1={5,6,8}; Gy2={11,1,13}; Gy3={14,14,17}. Sus respectivas medianas son:
$Mdy_1=6;Mdy_2=11;Mdy_3=14$
c) El punto $G=\left({\large{\frac{2+5+8}{3}}},{\large{\frac{6+11+14}{3}}}\right)=\left(5,{\large{\frac{31}{3}}}\right)$.
La pendiente de la recta es $p={\large{\frac{MdY_3-MdY_1}{MdX_3-MdX_1}}}={\large{\frac{14-6}{8-2}}}={\large{\frac{8}{6}}}={\large{\frac{4}{3}}}$.
De esta forma, la recta de Tukey será la de ecuación, $y={\large{\frac{4}{3}}}·(x-5)+{\large{\frac{31}{3}}}$
$y={\large{\frac{4}{3}}}·x+{\large{\frac{11}{3}}}$
Apartado ii) Recta de regresión (mínimos cuadrados)
Completamos los cálculos de nuestra tabla:
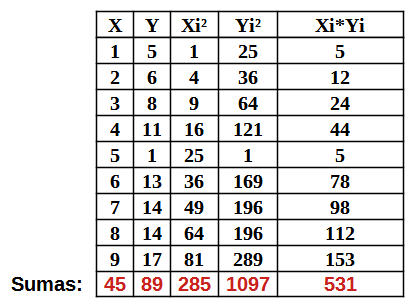
A partir de estos valores podemos obtener los parámetros:
$\bar{x}={\large{\frac{45}{9}}}=5$
$\bar{y}={\large{\frac{89}{9}}}$
$\sigma_x=\sqrt{{\large{\frac{285}{9}}}-5^2}=\sqrt{{\large{\frac{20}{3}}}}\approx 2.58$
$\sigma_y=\sqrt{{\large{\frac{1097}{9}}}-\left({\large{\frac{89}{9}}}\right)^2}=\sqrt{{\large{\frac{1952}{81}}}}\approx 4.91$
$\sigma _{x,y}={\large{\frac{531}{9}}}-5·{\large{\frac{89}{9}}}={\large{\frac{86}{9}}}\approx9.56$
En definitiva, la recta de ecuación $y={\large{\frac{\sigma_{x,y}}{\sigma_x^2}}}·(x-\bar{x})+\bar{y}$ será:
$y={\large{\frac{9.56}{6.67}}}·(x-5)+{\large{\frac{89}{9}}}\to \textbf{y=1.43328·x+2.72247}$ (Recta de Regresión)
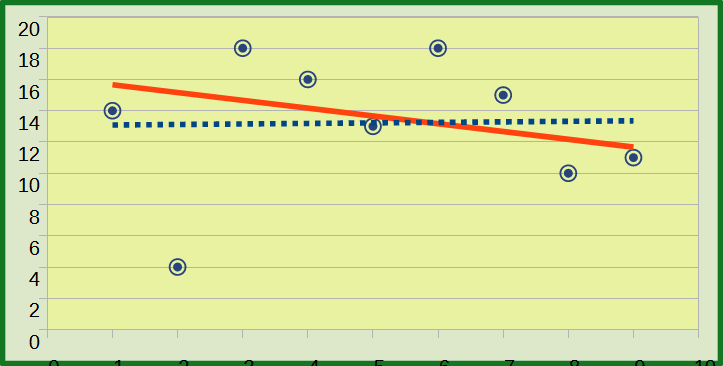
iii) Representa la nube de puntos y las dos rectas obtenidas.
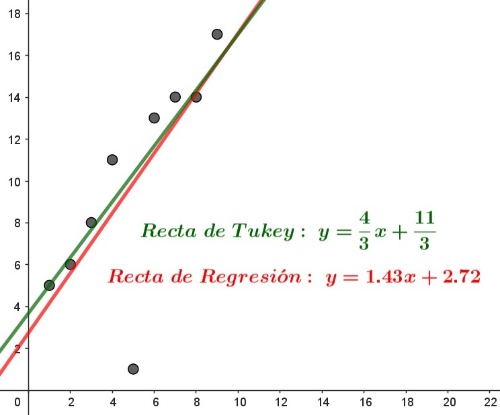
Ejercicio propuesto (opcional):
Sea la siguiente tabla de los datos obtenidos para una variable bidimensional.
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 14 | 4 | 18 | 16 | 13 | 18 | 15 | 10 | 11 |
a) Halla la recta de regresión de Y sobre X.
b) Calcula la recta de Tukey.
c) Representa la nube de puntos y las dos rectas obtenidas.
Nota: Si el número de datos n es múltiplo de 3, cada grupo está formado por n/3 datos.
Si el número de datos n no es múltiplo de 3, puede ocurrir que:
* Sea múltiplo de 3 más 1; el grupo G2 se deja con un dato más.
* Sea múltiplo de 3 menos 1; el grupo G2 se deja con un dato menos.
Ejercicio propuesto (opcional):
Sea la siguiente tabla de los datos obtenidos para una variable bidimensional.
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 14 | 4 | 18 | 16 | 13 | 18 | 15 | 10 | 11 |
a) Halla la recta de regresión de Y sobre X.
b) Calcula la recta de Tukey.
c) Representa la nube de puntos y las dos rectas obtenidas.
Respuestas:
a) $y=0.034x+13.05$
b) $y={\large{\frac{-1}{2}}}·x+{\large{\frac{97}{6}}}$
c) Recta de Tukey: Línea continua en rojo; Recta de Regresión: Línea punteada en azul.