5. Usamos distintos recursos tecnológicos

Estadística a través de GeoGebra:

Presentamos las características de GeoGebra como software educativo de carácter gratuito y libre que lo hacen especialmente interesante como herramienta informática para el análisis descriptivo de datos. La Hoja de Cálculo de GeoGebra se parece mucho a las de otros programas como Excel (Microsoft Office) o Calc (LibreOffice), conformada por columnas nombradas con las letras del alfabeto en mayúsculas y filas enumeradas, cuya intercepción igualmente, se denominan celdas. Cada celda se nombra por la letra de la columna y el número de la fila en la que se encuentra el indicador. Además de los comandos y opciones que GeoGebra nos ofrece, trabajaremos ahora con la aplicación Hoja de cálculo a la que accederemos a través del menú que aparecerá al pulsar sobre Vista. Es importante saber que los resultados generados en GeoGebra pueden ser exportados o copiados a otros programas. Basta presionar el botón derecho del ratón y seleccionar copiar en el portapapeles.

Construiremos una tabla con los valores de ambas variables X e Y, obteniendo todos los cálculos necesarios para hallar, si así es requerido, las medidas de centralización o de dispersión de ambas variables unidimensionales. De mayor interés será el estudio de la correlación entre ambas variables y el ajuste a un cierto modelo de regresión.

Iniciamos el trabajo con la Hoja de Cálculo de GeoGebra con algún ejemplo que nos permita conocer algunas de sus características y la forma de trabajar un conjunto de datos correspondientes a una variable estadística bidimensional para representar el diagrama de dispersión y determinar el modelo de regresión.  Proponemos la realización de este ejemplo:

Uso de GeoGebra como Hoja de Cálculo.

Ejemplo 1.- Se desea analizar con GeoGebra los siguientes datos que representan lecturas de la presión sistólica en mm-Hg, de 12 mujeres, en las edades que se indican:

EDAD (X):	22	27	29	32	35	40	48	50	51	57	67	71
PRESIÓN (Y):	131	106	123	122	121	147	115	163	138	141	176	172

a) Calcula el coeficiente de correlación lineal r y la recta de regresión mínimo cuadrática de la presión sobre la edad.
b) Según dicho modelo lineal, determina el valor de la presión para una mujer que tuviera 70 años.

A partir de los datos que se nos muestra en una tabla, GeoGebra nos ofrecerá los distintos parámetros estadísticos y mostrará gráficamente el Diagrama de Dispersión (nube de puntos) y la  representación de la Recta de regresión (Ver para ello el siguiente vídeo).

Estadística bidimensional con GeoGebra como Hoja de Cálculo.

Estadística bidimensional con GeoGebra

Estadística usando una Hoja de Calculo:

En este apartado vamos a realizar un ejercicio usando la hoja de cálculo del programa libre office que es software libre y que está disponible para todos los sistemas operativos, windows, linux o MAC.

Ejemplo 2 .- Encuentra la dependencia lineal y exponencial de la siguiente lista de datos sobre la población mundial (en millones de habitantes):
¿Cuál de ambos modelos se ajusta mejor a esta distribución?

Año X	Población (millones)
1750	728
1800	949
1850	1171
1900	1608
1950	2516
1997	5870

En las siguientes imágenes se representan las nubes de puntos de esta distribución bidimensional, con las dos interpretaciones que pide el problema, tratando una regresión lineal en la imagen de la izquierda y una exponencial en la de la derecha. Como se comprobará más tarde con los cálculos de los parámetros correspondientes, se ve a simple vista que los puntos se adecúan mejor a la exponencial que a la lineal. Como puede verse, la nube de puntos es la misma, pero la línea de ajuste es más próxima a los puntos en el modelo exponencial.

Estadística bidimensional con la hoja de cálculo CALC

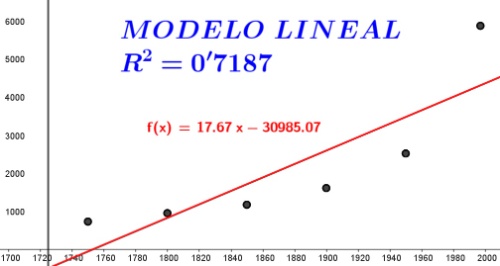
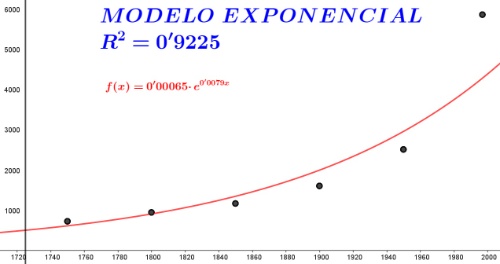
A la vista de los cálculos facilitados por la hoja de cálculo (CALC), podemos contestar a las preguntas realizadas:
MODELO LINEAL: $y=17,67·x-30985,07; \ r^2=0,7187$
MODELO EXPONENCIAL: $y=0,00065· e^{0,0079·x}; \ r^2=0,9225$
Por tanto, el modelo exponencial se ajusta mejor que el modelo lineal. (su valor de $r^2$ es considerablemente más próximo a uno).

Una aclaración importante: Fíjense que en los resultados del modelo exponencial se han puesto muchos decimales, la constante que multiplica tiene cinco cifras decimales y la del exponente cuatro. En muchas ocasiones nos preguntaremos ¿Cuántas cifras decimales debemos poner? No es una respuesta sencilla, pero al menos cada número debería tener como mínimo dos cifras significativas. Si recordamos la situación de aprendizaje que trataba de los números, se explicaba que un valor como 0,00065 tiene dos cifras significativas porque los ceros decimales a la izquierda no contaban como tales, y esto es importante porque si se pusiera solo 0,0006 se estaría cometiendo un error próximo al 10 % y cuando estos valores se arrastran en sucesivos cálculos pueden llegar a ser muy diferentes.

Estadística bidimensional usando calculadoras científicas:

En este apartado vamos a realizar un ejercicio usando diferentes tipos de calculadoras científicas desde las más recientes, que permiten ver la tabla de frecuencias mientras se van introduciendo los datos, hasta las más antiguas, que no dispones de esta ventaja pero que también permiten la introducción de datos estadísticos bidimensionales y que además nos proporcionan tanto los sumatorios como los parámetros estadísticos que estamos usando es esta Situación de Aprendizaje. A la hora de realizar una prueba escrita, esta herramienta resulta de interés ya que permite introducir en poco tiempo los datos y comprobar nuestros cálculos.

Ejemplo 3.- . Tenemos la siguiente tabla de datos de la temperatura media de varias ciudades y del gasto medio mensual en calefacción por habitante:

Temperatura (ºC): X	6	10	14	18	20	25
Gasto en calefacción (€): Y	50	45	25	15	10	2

a) Calcula el coeficiente de correlación y la recta de regresión de Y (gasto en calefacción) sobre X (temperatura media de la ciudad). 
b) Según el modelo obtenido, determina el valor del gasto previsible para una temperatura media de 15º.

Respuestas:
a) Recta de regresión: $y= –2,75x + 67,12$; $r=-0,982$
b) Para el valor de una temperatura media de 15º, obtendríamos un gasto aproximado de 25.87 €.

En el siguiente video se explican los pasos necesarios para realizar este ejercicio en la calculadora.

Ajuste lineal con un modelo de calculadora con pantalla

En el siguiente video se explican los pasos para realizar ejercicios de estadística bidimensional en diferentes tipos de calculadoras, desde una más antigua hasta la más reciente

Estadística bidimensional con modelo de calculadora sin pantalla