1. Entender la vida a través de los datos
Estadística bidimensional
En esta Situación de Aprendizaje se trabajan las distribuciones bidimensionales. En concreto, estudiaremos la forma de organizar la información en tablas de frecuencia, los parámetros que permiten interpretar dicha información, la correlación, que es la medida del grado de relación entre las variables, y la regresión, que estudia una variable condicionada al comportamiento de la otra.
1.- Dependencia entre las variables X e Y.
Al observar dos caracteres en cada individuo se presenta el problema de determinar la existencia de algún tipo de dependencia entre ellos. En este sentido, conviene destacar dos tipos de dependencia:
Dependencia funcional: Entre dos variables X e Y existe dependencia funcional cuando hay una expresión matemática que las relacione, existe una ley funcional que las relaciona entre sí. Por ejemplo, los radios de una circunferencia (X) y las longitudes (Y).
Dependencia aleatoria: Entre dos variables X e Y existe dependencia aleatoria cuando no existe una expresión matemática que las relacione. Por ejemplo, la edad de los niños (X) y la edad (Y).
Señalar que existen variables entre las que no existe ningún tipo de dependencia, ni funcional ni aleatoria, lo que conlleva a decir que los dos conceptos anteriores no son complementarios.
Puedes revisar a lo largo de esta Situación algún video explicativo de los conceptos que se van introduciendo y trabajando. Para ello te facilitamos el enlace a la página de píldoras matemáticas donde encontrarás muchos videos explicativos que esperamos te sean de gran utilidad.
2.- Estadística bidimensional.
Hasta ahora, hemos descrito el estudio que puede realizarse de una población o muestra respecto a una sola variable estadística. Lo que pretendemos ahora es abordar el estudio de un fenómeno respecto a dos variables unidimensionales simultáneamente. De este modo, se obtiene así el concepto de variable estadística bidimensional en la que cada elemento de la misma vendrá representado por un par ordenado $(x_i, y_i)$.
Parece lógico pensar que las siguientes parejas de variables deben guardar alguna relación entre sí:
- Los pesos y las estaturas de un conjunto de personas.
- El número de encuentros ganados por un equipo de fútbol y el lugar que ocupa en la clasificación.
- Las notas obtenidas por cada alumno de una clase en dos asignaturas de similares características.
- Las velocidades a las que circulan un conjunto de vehículos y su consumo de combustible.
- Extensión en $km^2$ y número de habitantes de los distintos países de Europa.
- Ingresos y gastos de cada una de las familias de los trabajadores de una empresa.
- Renta nacional y número de universitarios de los distintos países de África.
- Edad y número de días que faltan al trabajo los empleados de una fábrica.
- Número de horas que dedican los estudiantes a ver la televisión y resultados académicos.
A estas variables estadísticas resultantes de la observación de un fenómeno respecto de dos modalidades se las llama variables estadísticas bidimensionales. Las variables estadísticas bidimensionales las representaremos por el par (X,Y), donde X es una variable estadística unidimensional que toma los valores $x_1, x_2, x_3, ..., x_k$ e Y es otra variable estadística unidimensional que toma los valores $y_1, y_2, y_3 ,..., y_k$. Por tanto, la variable estadística bidimensional (X,Y) toma estos valores: $(x_1,y_1), (x_2,y_2),...,(x_k, y_k)$. Si representamos los valores de ambas variables en una tabla de dos filas o columnas obtendremos una especie de tabla de valores similar a las que nos encontramos en la representación gráfica de una función. Ello nos sugiere representarlos sobre dos ejes de coordenadas poniendo ${x_i}$ en abscisas e ${y_i}$ en ordenadas, obteniendo lo que llamaremos una nube de puntos o diagrama de dispersión. Existen, como hemos visto anteriormente, numerosas situaciones en nuestra vida real en los que se hace necesario estudiar simultáneamente dos variables.
En los siguientes apartados se detallan aspectos importantes referentes al por qué estudiar esta Situación de Aprendizaje en este curso, en qué parte pondremos especial atención y la interpretación del concepto de regresión.
1. ¿Justificación del estudio de esta Situación de Aprendizaje?
El estudio de la Estadística es fundamental por varias razones clave:
- Toma de decisiones informadas: La estadística proporciona herramientas para recopilar, organizar, analizar e interpretar datos. Esto permite a las personas y organizaciones tomar decisiones basadas en análisis sólidos en lugar de depender únicamente de intuiciones o suposiciones.
- Generalización y predicción: La estadística permite generalizar conclusiones sobre una población a partir de datos muestrales, lo que es esencial para hacer inferencias válidas sobre un grupo más amplio. Además, facilita la predicción de tendencias futuras y la evaluación de riesgos.
- Evaluación de la credibilidad: En un mundo inundado de información, la estadística ayuda a evaluar la credibilidad y la validez de los estudios y datos presentados. Proporciona herramientas para examinar la consistencia, fiabilidad y precisión de los resultados obtenidos.
- Investigación científica: En campos como la medicina, la economía, la psicología, entre otros, la estadística es fundamental para diseñar experimentos, analizar datos y sacar conclusiones significativas. Es una parte esencial del método científico y contribuye al avance del conocimiento en diversas disciplinas.
- Optimización de procesos y recursos: La estadística se utiliza en la gestión empresarial y la ingeniería para mejorar procesos, aumentar la eficiencia y minimizar costos. Permite identificar áreas de mejora y tomar medidas para optimizar recursos y aumentar la productividad.
- Control de calidad: En la fabricación y producción de bienes y servicios, la estadística es esencial para controlar la calidad y garantizar que los productos cumplan con los estándares establecidos. Ayuda a detectar y corregir problemas en la producción antes de que afecten a los consumidores.
En resumen, el estudio de la estadística es importante porque proporciona las herramientas necesarias para comprender y analizar datos de manera efectiva, tomar decisiones informadas, realizar predicciones válidas y contribuir al avance del conocimiento en una variedad de campos.
2. ¿En qué pondremos el énfasis?
La Estadística se puede interpretar como la confluencia de dos análisis: el descriptivo y el inferencial. En esta situación, abordaremos el estudio de la Estadística Descriptiva, para así poner la base del segundo análisis, basado en el cálculo de probabilidades.
En el estudio de la Estadística Descriptiva, se pone el foco en la comprensión y descripción de los datos de manera clara y concisa. Aquí presentamos algunos aspectos en los que incidiremos:
- Resumen de datos: La Estadística Descriptiva se centra en resumir grandes conjuntos de datos de manera que proporcionen información útil y comprensible. Esto implicará calcular medidas de tendencia central (como la media, la mediana y la moda) y medidas de dispersión (como la varianza, la desviación típica y el rango) para describir la distribución de los datos.
- Visualización de datos: Se hará hincapié en la representación visual de los datos utilizando gráficos y diagramas apropiados. Esto incluye histogramas, diagramas de barras, diagramas de dispersión y diagramas de caja, entre otros. Estas representaciones nos ayudarán a comprender la forma de la distribución, identificar valores atípicos y patrones en los datos.
- Exploración de relaciones entre variables: La Estadística Descriptiva también se utiliza para explorar las relaciones entre diferentes variables en un conjunto de datos. Esto implica calcular correlaciones y covarianzas para medir el grado y la dirección de las relaciones de dependencia (estadística) entre aquéllas variables.
- Identificación de valores atípicos: Se presta atención a la identificación y el manejo de valores atípicos o extremos en los datos, ya que pueden sesgar las conclusiones y los análisis. Esto implica calcular los valores atípicos utilizando métodos estadísticos apropiados y decidir cómo tratarlos adecuadamente en el análisis.
- Interpretación de resultados: Se enfatiza la capacidad de interpretar los resultados de manera significativa y relevante para el contexto en el que se están utilizando los datos. Esto implica comprender qué significan las medidas estadísticas en términos prácticos y cómo se pueden utilizar para respaldar conclusiones o tomar decisiones.
En general, el énfasis en el estudio de la Estadística Descriptiva radica en comprender y comunicar de manera efectiva la información contenida en los datos, lo que es fundamental para cualquier análisis estadístico posterior y para una eficiente toma de decisiones.
3. Regresión: Cálculo e interpretación.
Atletismo. 1 500 metros lisos masculinos.
La carrera de los 1 500 m lisos es en la actualidad la prueba estrella del atletismo de medio fondo. La modalidad masculina forma parte de los Juegos Olímpicos modernos desde su primera edición, que tuvo lugar en Atenas en 1896. En dicha edición resultó vencedor el australiano Edwin Flack, quien obtuvo un registro de 4’ 33,2’’. La modalidad femenina no fue reconocida hasta las Olimpiadas del año 1972, en las que resultó vencedora la soviética Lyudmila Bragina, con un tiempo de 4’ 01,38”. El atleta que ganó esta prueba en los Juegos Olímpicos, celebrados en Brasil, en el año 2016, fue el estadounidense Matthew Centrowitz, con un tiempo de 3’ 50’’. Actualmente, el récord mundial lo ostenta el marroquí Hicham El Guerrouj, quien obtuvo en Roma, en junio del año 1988, la extraordinaria marca de 3’ 26,17”.

La tabla que te presentamos recoge las marcas olímpicas de 1500 m masculinos desde Atenas 1896 hasta Río de Janeiro 2016:
| AÑO | MARCA (min.) | AÑO | MARCA (min.) | AÑO | MARCA (min.) |
| 1896 | 4,553 | 1948 | 3,83 | 1988 | 3,599 |
| 1900 | 4,103 | 1952 | 3,752 | 1992 | 3,678 |
| 1904 | 4,09 | 1956 | 3,687 | 1996 | 3,596 |
| 1908 | 4,057 | 1960 | 3,593 | 2000 | 3,535 |
| 1912 | 3,947 | 1964 | 3,635 | 2004 | 3,570 |
| 1920 | 4,03 | 1968 | 3,582 | 2008 | 3,549 |
| 1924 | 3,893 | 1972 | 3,605 | 2012 | 3,569 |
| 1928 | 3,887 | 1976 | 3,653 | 2016 | 3,833 |
| 1932 | 3,853 | 1980 | 3,64 | ||
| 1936 | 3,797 | 1984 | 3,542 |
Dibujamos un diagrama de puntos que represente la información:
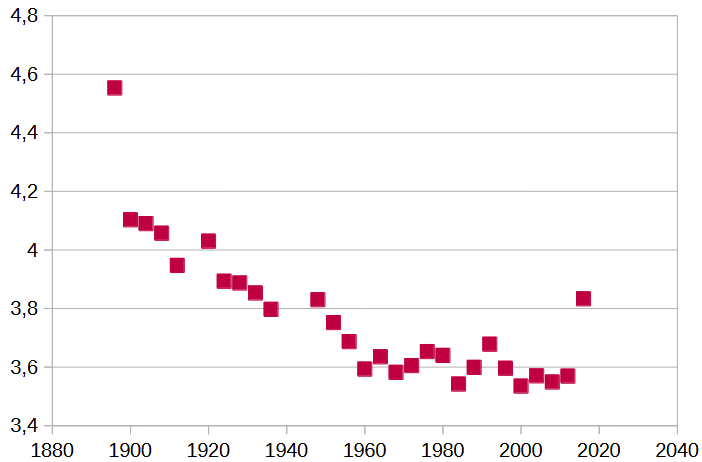
- ¿Crees que los datos presentan una tendencia lineal? Justifica tu respuesta.
- Dibuja una recta que represente la nube de puntos. ¿Sabes cómo se llama esta recta?
- Obtén la expresión analítica de la recta anterior.
- ¿En qué años no se celebraron olimpiadas? ¿Sabes por qué?
- ¿Podrías predecir las marcas de los años olímpicos que faltan? Explica cómo lo harías.
- ¿Crees que es razonable utilizar la recta de regresión para estimar la marca en los juegos olímpicos de 2048? ¿Por qué?¿Y para los del 2200? ¿Por qué?
Todas estas cuestiones y otras más quedarán resueltas en esta Situación de Aprendizaje. ¡Síguenos y lo comprobarás!
La difusión de los métodos estadísticos puede contribuir a una sociedad más abierta, más liberal y más tolerante
Daniel Peña
