1.2. Equilibrio simultáneo. Sistemas
 |
| Lupa Watson de DaRoit, CC by-nc-sa 2.0 |
En las dos situaciones mostradas en el punto anterior no hemos podido más que establecer una relación entre las dos incógnitas y dar posibles combinaciones de resultados.
Pero, ni hemos podido determinar un número único de goles marcados por cada uno de los delanteros del F.C Barcelona, ni el número preciso de goles marcados por cada uno de los equipos.
En ambas situaciones nos falta una pista: otra ecuación. Al tener dos incógnitas, para poder encontrar unos valores únicos para los goles marcados, necesitamos al menos dos pistas, es decir dos ecuaciones.
Si las dos pistas son "buenas", entonces sí que podremos encontrar unos valores únicos para las incógnitas planteadas.
Con las dos pistas tendremos lo que en matemáticas se conoce con el nombre de sistema de ecuaciones.
Actividad
Un
sistema de dos ecuaciones lineales con dos
incógnitas, como su propio nombre indica, está compuesto por dos ecuaciones de primer grado.
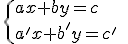
Resolver el sistema es encontrar una solución común de ambas ecuaciones. Por tanto, una solución del sistema es una pareja de valores (x,y) que cumple ambas ecuaciones de manera simultánea.
Actividad
Si interpretamos ésto desde un punto de vista gráfico, una solución del sistema vendrá dada por las coordenadas (x,y) de un punto que pertenezca a las dos rectas, esto es, de un punto de corte de las dos rectas.
Por tanto, para resolver un sistema de ecuaciones, por el método gráfico, debemos:
- Representar gráficamente la recta de cada una de las ecuaciones.
- Determinar los puntos comunes de ambas rectas.
En la siguiente escena de geogebra puedes ver la representación gráfica de una ecuación lineal con dos incógnitas.
En esta otra puedes ver la interpretación gráfica de la solución de un sistema de dos ecuaciones con dos incógnitas.
A la hora de resolver un sistema de dos ecuaciones con dos incógnitas por el método gráfico se procede de la siguiente forma.
Por ejemplo, consideremos el sistema:
Vamos a despejar la "y" de cada una de las ecuaciones:
 |
Ahora, en una tabla, daremos valores a la "x", y realizando las operaciones obtendremos los correspondientes valores de la "y". Así, conseguiremos las coordenadas (x, y) de algunos puntos de cada recta, y uniéndolos obtendremos sus gráficas.
|
|
||||||||||||||||||||
La solución del sistema es el punto donde se cortan las dos rectas, como podemos ver en la tabla, dicho punto es A(-1, 6), es decir, la solución es: x = -1 y = 6.
Veamos la representación gráfica de este sistema y su solución, hemos llamado "a" a la recta: ![]() , "b" a la recta:
, "b" a la recta: ![]() , y A(-1, 6) es el punto de corte de las dos rectas a y b.
, y A(-1, 6) es el punto de corte de las dos rectas a y b.
Fuente propia bajo Dominio público
|
Como puedes ver, dibujar las rectas de cada una de las ecuaciones no es una tarea excesivamente compleja. Basta despejar y en función de x, elaborar una pequeña tabla de valores y representar los puntos obtenidos.
En la siguiente presentación, se explica cómo puedes resolver sistemas de ecuaciones con Wiris de manera analítica.