Ejercicio 14

 

 

El hockey sobre hielo es un deporte que se juega entre dos equipos de seis jugadores, con patines sobre una pista de hielo. Los patinadores deben dirigir un disco de caucho, para tratar de anotar en la portería del rival. Los jugadores pueden realizar cargas con el cuerpo sobre el rival, para tratar de arrebatarle el control del disco, por lo que suelen ir equipados con toda clase de protecciones. Es también uno de los juegos más rápidos, debido a que la fricción del disco y de los patines sobre el hielo es mínima.

Ahora vamos a ver la importancia de las protecciones que llevan los jugadores. Para ello supón que eres un portero de hockey y estás delante de Dion Phaneuf, quién posee el lanzamiento más rápido de la NHL 162 km/h. El disco de hockey tiene una masa de 173 g y a la distancia que Dion Phaneuf va a lanzarte el disco, sabes que éste apenas perderá velocidad. Si al parar el lanzamiento el disco está en contacto con el guante 0,5 s.

a) Calcula la fuerza que ha de ejercer tu mano para parar el disco.

La fuerza que tendrá que realizar la mano del portero para detener el disco será igual a la variación por unidad de tiempo de la cantidad de movimiento del disco.

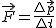
El módulo de la fuerza aplicada vendrá dado por la expresión:

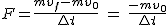
Pasamos la velocidad del disco a m/s y su nasa a Kg para poder sustituir en la expresión anterior:

v₀ = 162 km/s = 45 m/s

m = 173 g = 0,173 kg

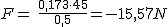
b) Compara esta fuerza con el peso del disco e indica cuántas veces es mayor.

El peso del disco es:

P = m·g = 0,173·9,8 = 1,7 N

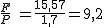
La fuerza que ejerce la mano sobre el disco es 9,2 veces mayor que su peso.

c) Si el guante triplica el tiempo de contacto entre el disco y la mano ¿cuántas veces soportarías el peso del disco si lo pararas sin llevar guantes?

El impulso que recibe el disco será igual a la variación de su cantidad de movimiento:

I = F·Δt = Δp = mv_f-mv₀ = 0 – 0,173·45 = - 7,785 N

Si el guante triplica el tiempo que actúa esta fuerza, en caso de no llevar guante el tiempo que actúa esta fuerza es:

Δt = 0,5/3 = 0,167

Y la fuerza aplicada sería:

I = FΔt; F = I/Δt = -7,785/0,167 = - 46,62 N

Ésta sería la fuerza ejercida por tu mano sobre el disco. Teniendo en cuenta el tercer principio de la dinámica, tu mano recibiría una fuerza igual y de sentido contrario.

Comparándolo con el peso del disco:

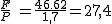
La fuerza que se ejerce para conseguir esta variación de la cantidad de movimiento actúa.

 

Los choques entre los jugadores de hockey son comunes y a la velocidad que se mueven estos, si no fuera por las protecciones que llevan serían muy peligrosos. Pero no solamente es importante llevar unas buenas protecciones la masa de los jugadores también tiene su importancia. Vamos a comprobarlo. Imagina que estás en un partido de hockey y ves uno de estos choques entre jugadores. Uno de masa 105 Kg y que se mueve a 7 m/s choca con otro que de igual masa y que está parado. Después del choque el primer jugador queda parado y el otro sale disparado.

Debido al escaso rozamiento del hielo podemos considerar que se cumple el principio de conservación de la cantidad de movimiento.

 

Antes del choque: m₁·v₁ + m₂·v₂

Después del choque: m₁·v´₁ + m₂·v´₂

Suponemos que el choque se produce de forma frontal y en una sola dirección:

m₁·v₁ + m₂·v₂ = m₁ v´₁ + m₂·v´₂

Sustituimos los valores:

105·7 + 105·0 = 105·0 + 105·v´₂

735 = 105 v´₂; v₂ = 735/105 = 7 m/s

Al colisionar dos jugadores de igual masa se intercambian la cantidad de movimiento.

b) Si fueras tú el jugador que está parado en la pista y que recibe el golpe ¿con qué velocidad te moverás?

En este caso la masa del segundo jugador sería de 90 Kg.

m₁·v₁ + m₂·v₂ = m₁ v´₁ + m₂·v´₂

105·7 + 90·0 = 105·0 + 90·v´₂

735 = 90 v´₂; v₂ = 735/90 = 8,2 m/s

Me movería con una rapidez de 8,2 m/s