4.4. Fracciones algebraicas. Operaciones
Actividad
Una fracción algebraica está formada por el cociente de dos polinomios 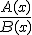
Dos ejemplos de fracciones algebraicas son
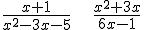
|
La elegancia es fundamental dentro del mundo matemático por lo que las fracciones algebraicas se presentan simplificadas. Para ello, descomponemos el numerador y el denominador en factores irreducibles, eliminando los factores que coinciden.
Veamos un ejemplo, en el que simplificamos la expresión
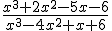
|
Factorizamos x3+2x2-5x-6=(x+1)·(x-2)·(x+3) y x3-4x2+x+6=(x+1)·(x-2)·(x-3) para obtener
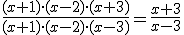
|
Caso de estudio
Simplifica la expresión algebraica
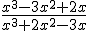
|
Caso de estudio
Simplifica esta otra expresión algebraica
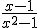
|
Actividad
-
Fraciones con igual denominador.
La suma o resta de fracciones con idéntico denominador, es una fracción cuyo numerador es la suma o resta de los numeradores y cuyo denominador es el mismo denominador de las fracciones. Es decir:
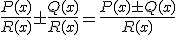
|
-
Fracciones con distinto denominador.
Si las fracciones algebraicas tienen diferente denominador, construiremos nuevas fracciones equivalentes con identicos denominador, siendo este el m.c.m. de los denominadores. Los numeradores correspondientes a los resultado de dividir el m.c.m por el denominador, multiplicado por el numerador previo. Es decir: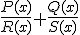
y sea
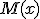 el m.c.m. de
el m.c.m. de 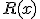 y
y 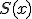
El resultado obtenido es
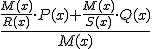
Análogamente se opera con la resta.
Actividad
- Multiplicación de fracciones algebraicas
Al multiplicar dos fracciones algebraicas, obtenemos una nueva fracción algebraica cuyo numerador es el producto de los dos numeradores y el denominador el producto de los denominadores.
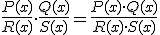
|
Actividad
Para dividir dos fracciones algebraicas, multiplicamos la primera fracción algebraica por la inversa de la segunda.
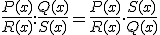
|