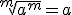1.3. Potencias y raices
Actividad
Dado un número a y un número natural n, llamamos potencia de base a y exponente n, al número
an = a·a·a·a·a·a...·a (n veces)
que se consigue multiplicando la base a, por sí misma tantas veces como indique el exponente n.
Ejemplo
24 = 2·2·2·2 = 16; 65 = 6·6·6·6·6 = 7776; 48 = 4·4·4·4·4·4·4·4 = 65536
La potencia x2 se llama cuadrado y la potencia x3 se llama cubo. Las siguientes se llaman potencia cuarta, quinta, sexta... En general, xn se llama enésima potencia o n-ésima potencia.
Actividad
La radicación u obtención de raíces es la operación contraria a elevar un número a una potencia. Se expresan con el símbolo radical: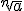 
El valor que aparece dentro del símbolo radical se llama radicando, y la cantidad que aparece encima del radical se llama índice de la raíz. Esta expresión nos indica el número que al elevarlo a n nos de el número a, es decir: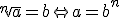 
Cuando en un radical no se expresa el índice, por convenio se establece que se está calculando una raíz cuadrada. Es decir, se escribe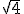 
en lugar de 
.
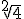Actividad
Propiedades de las potencias de exponente natural
En la siguiente tabla están resumidas las propiedades de las potencias vistas anteriormente:
|
Actividad
Propiedades de las potencias de exponente entero
Las potencias de exponente entero verifican las mismas propiedades que las potencias de exponente natural. Además de estas, también verifican la propiedad vista más arriba, que resumimos en la siguiente tabla, en la que aparece también la importante propiedad de una potencia con exponente cero:
| Potencia con exponente cero |  |
| Potencia con exponente cero |  |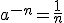
Otra propiedad de las potencias, aunque puede parecer obvia, hay que tenerla clara y es que 
Actividad
Propiedades de las potencias de exponente fraccionario
Las potencias de exponente fraccionario heredan las mismas propiedades que las vistas en los apartados anteriores. Además añaden la que acabamos de deducir:
| Potencia de exponente fraccionario |
 |
Actividad
Las principales propiedades que verifican las raíces son las que se indican en la siguiente tabla, y se deducen al aplicar las propiedades de las potencias:
| Producto de raíces del mismo índice |
|
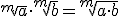
| Cociente de raíces del mismo índice |
|
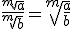
| Raíz de una raíz |
|
| Raíz de una potencia |
|
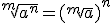
| Simplificación |
|
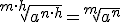
De la propiedad de simplificación se deduce otra propiedad que aplicamos continuamente: 