2.1. Nociones básicas sobre el cálculo de primitivas
Ya sabemos que la integración es el proceso inverso de la diferenciación o derivada. Por este motivo, conociendo las propiedades de las derivadas y la tabla de derivadas de las funciones, conocemos también la función integral de algunas funciones específicas sencillas.
Vídeo de Mariano Real Pérez alojado en YouTube
Ejemplo:
Una rápida lectura de la definición de primitiva nos lleva a pensar que integrar una función es el proceso inverso de derivar. Al integrar una función f(x) obtenemos una nueva función F(x), a la que llamaremos primitiva de la anterior, y que, al derivarla, se obtiene la función de partida. Veamos esto con un ejemplo:
Sabemos que (x3)'=3x2, así pues:
![]()
donde C es una constante cualquiera.
Podemos observar que, si f(x) = 3x2, tendremos que su primitiva es F(x) = x3 + C, cumpliéndose que F'(x) = f(x).
AV - Actividad de Espacios en Blanco
Dadas las siguientes integrales, seguro que ya eres capaz de asociarlas con sus respectivas primitivas a partir de la definición:
a) 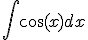
b) 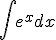
c) 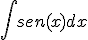
Identifica la solución de cada una de ellas por su letra.
Importante
Recuerda que siempre puedes comprobar si el resultado obtenido es correcto derivando la función primitiva. Si obtienes el integrando la solución es correcta.
Te recordamos que en esta calculadora para comprobar tus cálculos. En la pestaña Derivar puedes seleccionar también integrar.
Si no te funciona correctamente pincha en este enlace.