1.2. Relaciones entre las razones trigonométricas
Fórmula fundamental de la trigonometría
Dado el triángulo de la figura
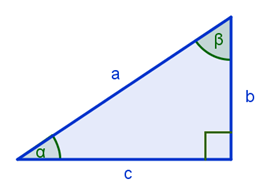
sabemos que 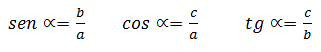
Si ahora partimos del teorema de Pitágoras a2= b2+ c2
Dividimos la expresión por a2 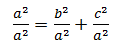
Sustituimos por sus valores y obtenemos ![]()
Actividad
Se conoce como fórmula fundamental de la trigonometría a la siguiente expresión que relaciona el seno y el coseno de un ángulo:
![]()
Relación de la tangente con el seno y el coseno
Si ahora dividimos el seno y el coseno del ángulo ![]()
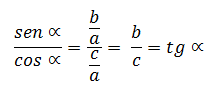
Así quedan relacionados el seno, el coseno y la tangente de un ángulo
Actividad
La tangente, el seno y el coseno de un ángulo se relacionan a través de la expresión siguiente:
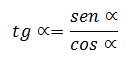
PRACTICA TÚ
Practica las relaciones fundamentales de la trigonometría
| Escena de Consolación Ruiz en Proyecto Descartes. Licencia CC |
Caso práctico
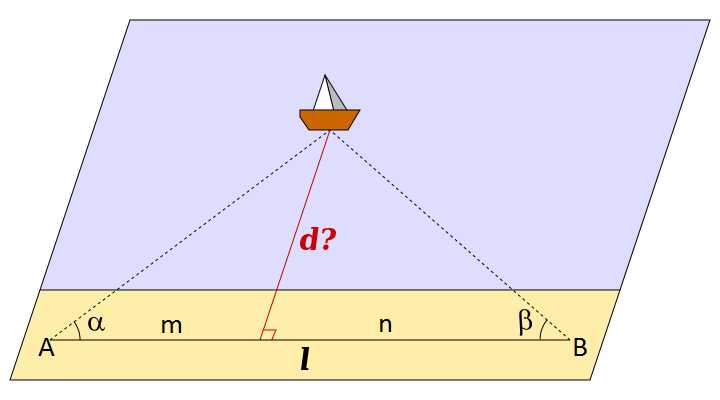
Vamos a aplicar el cálculo de distancias usando la triangulación. Queremos conocer la distancia a la que se encuentra el barco de la imagen, sabiendo que la distancia que separa los puntos de observación l = 1500 metros. Los ángulos de observación son α = 50º y β = 45º.
 |
| Imagen de R. Lachaume en Wikimedia Commons. Licencia CC |
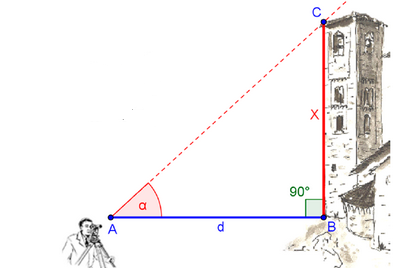
Vamos a calcular la altura de una torre sabiendo la distancia que la separa del observador y el ángulo de observación. En este caso d = 250 m y α=20º.
 |
| Captura de pantalla de 3con14.com. Licencia CC |
Objetivos
