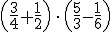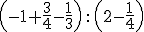4.1 Operaciones, ordenación y representación

Nuevos números, nuevas formas de expresarlos: las fracciones.

Una fracción es un compendio de dos números enteros $\frac{a}{b}$ , siendo b distinto de 0. El superior se denomina numerador y el inferior denominador. Este indica las partes en que se ha dividido la unidad o si se prefiere denomina el tipo de subunidad. El numerador indica el número o cantidad de subunidades a considerar. Así un minuto es la sesentava parte de una hora, $\frac{1}{60}$ y 3 minutos se dirá $\frac{3}{60}$ de hora.

Uno de los problemas que plantean las fracciones es que una misma medida (un mismo número) puede expresarse de formas distintas. Así media hora puede expresarse también como 30 minutos, $\frac{30}{60}$ de hora. Los matemáticos llaman número racional a lo que tienen en común todas las fracciones que describen la misma medida.

Podría decirse que cada número racional es único aunque admite muchas expresiones fraccionarias, muchos disfraces.

Actividad

Los números enteros se consideran una parte de los números racionales. Si a es un número entero, podemos expresarlo en forma de fracción:

$a=\frac{a}{1}$

Fracciones equivalentes. Operaciones con fracciones.

Las fracciones equivalentes serán el concepto en el que nos basaremos para comparar, sumar y restar fracciones, ya que podremos buscar siempre fracciones equivalentes a las dadas que entre ellas tengan el mismo denominador, lo que será la clave para poder operar con ellas.

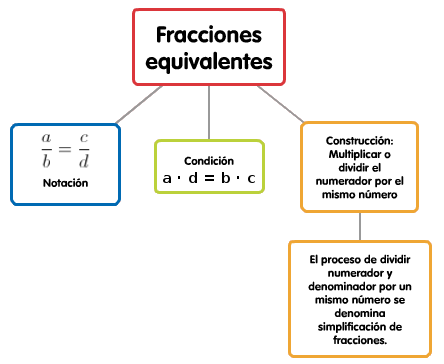Imagen de elaboración propia

$Ejemplo fracciones equivalentes$

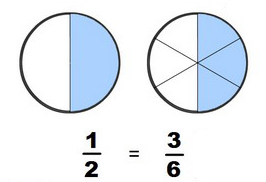Imagen de elaboración propia

En la siguiente presentación te mostramos cómo puedes realizar estas y otras operaciones. Además, la acompañamos por un vídeo de juanmemol, en el que realiza una actividad de operaciones combinadas con fracciones.

Por cierto, ¡por fin podemos hablar con toda tranquilidad de la división entre números enteros!

Con la presentación anterior, a través de la comparación de funciones, ya te habrás dado cuenta que las fracciones también se pueden ordenar en la recta real, pues existe una relación de orden entre ellas. En la siguiente escena de Geogebra, puedes descubrir esta propiedad:

Caso de estudio

El profesor de matemáticas suele desayunar en la cafetería del instituto: "Por favor, un café y media de tomate". Su amiga Paqui, que quiere que la invite a desayunar: "Para mi otra media". El camarero trae una tostada completa. Paqui sonríe, nunca entiende las bromas del camarero.

En una mesa, mientras se toma su bocadillo, Meki, una chica del instituto, llama a su profe: "Esto debe estar mal, me salen tres cuartos y no se puede dividir". Paqui, que es profe de francés pero suele hacer la compra de su casa, salta: "Pues claro que se puede, ayer compré tres cuartos de kilo de carne y me pusieron 750 gramos". Suena el timbre y todos a clase.

El profesor sabe que en su próxima clase encontrará más chicas que chicos. 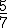del grupo son chicas y en total son 28. ¿Cuántas chicas hay en esa clase?

Paqui debe ir al cajero a sacar dinero. Piensa que si gasta 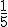de su dinero en la entrada para un coche, 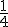en comprarse los muebles que necesita, la décima parte de sus ahorros en un ordenador y 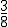de los mismos en liquidar lo que le falta para terminar de pagar su casa, aún le quedarán 375 €. "No está nada mal", piensa ella. Por cierto, ¿cuánto dinero tiene Paqui?

Por su parte, Meki que tiene 250 € ahorrados, piensa gastarse 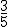de su dinero en ropa, 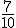de lo que aún le quede en música y 30 € en un libro. Lo que le sobre se lo regalará a su hermana. ¿Es muy generosa con su hermana?

El profesor de matemáticas debe corregir los exámenes de una clase. Ayer corrigió 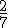de todos los exámenes, hoy piensa corregir 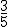de los que le quedan, y así para mañana sólo le restarán 8. ¿Cuántos alumnos/as se presentaron al examen?.