3.2. Múltiplos y divisores

Fotografía en Flickr por osolev bajo CC

Múltiplos y divisores. Divisibilidad

Frente a lo que pudiera parecer la operación producto de números enteros ha tenido mayor importancia que la suma. El producto ha permitido un mayor conocimiento de los números enteros e interesantes aplicaciones prácticas. Por ejemplo, la clasificación de los números primos, que son esenciales en las labores de codificación en informática y en la creación de claves.

Actividad

Si 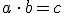con y 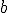números enteros distintos de 0, entonces

y 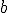se llaman divisores o factores de . También se dice múltiplo de y .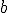

Dado que 2·5=10, 2 y 5 son divisores o factores de 10. A su vez 10 es un múltiplo de 2 y de 5.
Decir que 2 es un divisor de 10 es equivalente a decir que 10 es un múltiplo de 2.

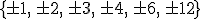es el conjunto de los divisores de 12.

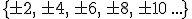es el conjunto de los múltiplos de 2, también llamados números pares.

Observa que un número tiene infinitos múltiplos, mientras que el número de divisores es finito. Por eso podemos hablar del máximo común divisor (m.c.d.) y del mínimo común múltiplo (m.c.m).

El m.c.d de varios números enteros es el mayor de los divisores comunes a todos ellos.
Se llama m.c.m. de varios números enteros al menor de los múltiplos comunes a todos ellos.

En la siguiente escena de Geogebra calculamos el m.c.m y el m.c.d de dos números:

Hay unos criterios de divisibilidad que nos permiten reconocer sin realizar operaciones si un números es divisible por otro. A continuación te damos los más frecuentes y sencillos de aplicar:

PDF alojado en 3con14. Licencia CC

Números primos y compuestos. Una nueva clasificación de los enteros.

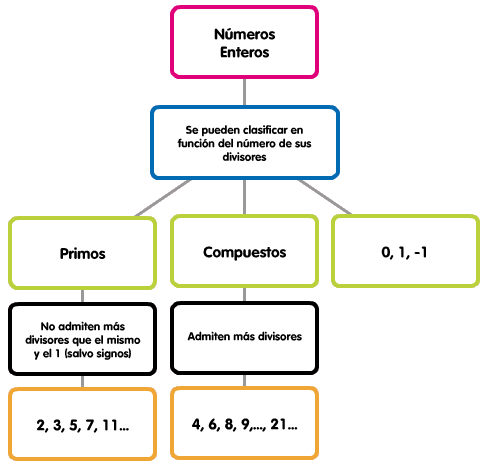
Ya hemos agrupado los números enteros en: enteros positivos, enteros negativos y el 0. Pero utilizando la noción de divisibilidad, podemos agruparlos en: primos, compuestos y casos especiales como el 1, -1 y 0.

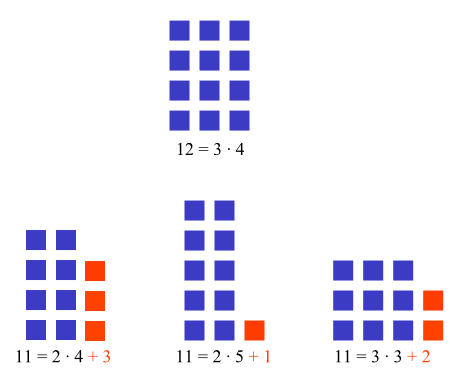
Intuitivamente un número n es primo si al colocar n objetos en cajas rectangulares la única disposición posible fuera 1 por n. Si existiera otra disposición el número se denomina compuesto:

Imagen de elaboración propia

Imagen en Wikimedia Commons de TakuyaMurata bajo Dominio Público

Actividad

Todo número compuesto se descompone en producto de números primos de forma única (no teniendo en cuenta el orden de los factores, ni las unidades 1). A la descomposición en factores primos también se le llama factorización.

Este resultado es tan importante que ha adoptado el nombre de Principio Fundamental de la Aritmética. Los números primos serían, pues, como los ladrillos, los átomos que con la ayuda del producto permiten construir el edificio de la aritmética.

Veamos un ejemplo:

La factorización de los números es muy útil a la hora de calcular el máximo común divisor y el mínimo común múltiplo.

Pasos a seguir en el cálculo del m.c.d. de varios números enteros:

Se descompone cada uno en factores primos.
Cada número se expresa como producto de factores primos en forma exponencial.
El m.c.d. es el producto de aquellos factores primos comunes a todos ellos tomados con su menor exponente.

Pasos a seguir en el cálculo del m.c.m. de varios números:

Se descompone cada uno en factores primos.
Cada número se expresa como producto de factores primos en forma exponencial.
El m.c.m.es el producto de aquellos factores primos comunes y no comunes a todos ellos tomados con su mayor exponente.

Caso de estudio

En mi casa tengo una pared de 435 cm de largo por 240 cm de alto. Deseo cubrirla entera con azulejos de forma cuadrada, todos del mismo tamaño, y usando el menor número posible de ellos (sin romper ninguno).

¿La medida del lado de los azulejos será múltiplo o divisor del largo y del alto de la pared?

La longitud buscada para el lado del azulejo, por tanto, será un divisor de ambos lados y el azulejo debe ser lo más grande posible (para utilizar el menor número de azulejos). Luego, buscamos el MÁXIMO COMÚN DIVISOR de las longitudes de los lados. Intenta calcularlo.

Caso de estudio

En nuestro instituto funcionan cinco talleres: fotografía, ajedrez, canto, teatro y literatura. Las reuniones del taller de fotografía se hacen cada dos días; el de ajedrez cada tres; el de canto cada cuatro días; el de teatro cada cinco días y el de literatura cada seis días.

Si el día 1 de Octubre se reunieron los cinco talleres, ¿cuándo será la próxima vez en que volverán a coincidir las reuniones de todos los talleres?.

Retroalimentación

Observa que el número buscado debe ser múltiplo de los 5 números dados, ya que un taller se reúne cada vez que suma una cantidad fija de días, es decir, va construyendo un serie de múltiplos (p.e. ajedrez se reúne a los 3 días, a los 6 días, a los 9 días, ..., el de teatro a 5 días, a los 10, a los 15,...).

Por tanto, queremos un múltiplo común, y deseamos saber la primera vez que ocurrirá, luego, buscamos el MÍNIMO COMÚN MÚLTIPLO.

Como hemos visto antes, descomponemos todos los números en factores primos y tomamos los factores comunes y no comunes con mayor exponente. De ese modo es múltiplo de todos y es el más pequeño posible.

Pues bien haciendo eso, obtenemos que 2,3 y 5 son números primos, 4 = 2² y 6 = 2·3; Por tanto el mínimo común múltiplo es 2²·3·5, o lo que es lo mismo 60.

Luego cada 60 días vuelven a coincidir. Si coincidieron el día 1 de octubre, la próxima vez será el 30 de noviembre.