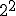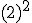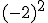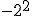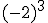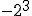3.1. Operaciones, ordenación y representación
Enteros: una ampliación de los naturales. Comparación y ordenación.
Los números enteros pueden considerarse la segunda etapa de ese viaje alucinante que ha comenzado con los números naturales. Entran en escena cuando hay un antes y un después, un arriba y abajo, derecha e izquierda, haber y deber...
 |
| Fotografía en Flickr por Andrea bajo CC |
Al graduar la recta con los números naturales adoptábamos un origen y una unidad. Los números naturales hacían su aparición al llevar la unidad en el mismo sentido a partir del origen. Pero ¿qué ocurre si el sentido se invierte? Hacen su aparición los números enteros negativos, simétricos u opuestos de sus hermanos, los números naturales, ahora también llamados números enteros positivos.
 |
| Imagen de elaboración propia |
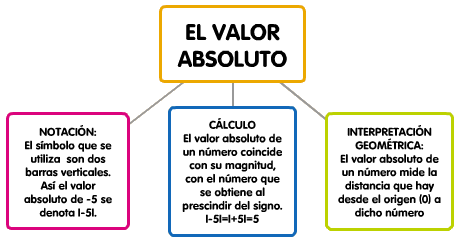
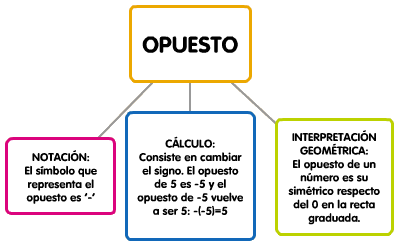
Con los números enteros introducimos dos operaciones nuevas, que condicionarán el uso de las que ya conocíamos: el valor absoluto y el opuesto.
 |
| Imagen de elaboración propia |
|
|
| Imagen de elaboración propia |
El valor absoluto y el opuesto son operaciones unarias, pues sólo necesitan un operador (|| o -) y un único operando.
Aunque con la representación en la recta real, ya te habrás hecho una idea de que mayor es un número cuanto más a la derecha esté situado, esto se puede resumir en un lenguaje más formal de la siguiente manera:
- De dos números enteros positivos es mayor el que tiene mayor valor absoluto: +13 > +3.
- Cualquier número entero positivo es mayor que cero: +11 > 0.
- Cualquier número entero positivo es mayor que cualquier número entero negativo: +3 > -15.
- El cero es mayor que cualquier número entero negativo: 0 > -11.
- De dos números enteros negativos es mayor el que tiene menor valor absoluto: -8 > -25.
AV - Pregunta Verdadero-Falso
Retroalimentación
Verdadero
Porque tiene la misma magnitud.Retroalimentación
Falso
El valor absoluto de un número es la distancia entre ese número y el 0. La distancia es una magnitud que siempre es positiva.Retroalimentación
Verdadero
Para obtener el opuesto sólo hay que cambiar el signo.Operaciones con números enteros
Aunque el valor absoluto y el opuesto también son operaciones, este apartado lo dedicaremos a las operaciones "clásicas" (por clásicas no nos referimos a más antiguas, pero sí seguro que a las que más recuerdas).
Además las primeras operaciones pueden ampliar la definición de las operaciones suma y producto al conjunto de los números enteros.
En el caso de la suma de dos números enteros distinguimos dos casos:
- Que ambos números tengan el mismo signo. En este caso el signo del resultado es el signo común de los sumandos. El valor absoluto del resultado es la suma de los valores absolutos de los sumandos.
- Que los números a sumar tienen distinto signo, el resultado adopta el signo del sumando de mayor valor absoluto. El valor absoluto del resultado es la diferencia entre el mayor valor absoluto de los sumandos y el menor.
La operación resta o diferencia entre números enteros se puede entender como un caso particular de la suma: a-b=a+(-b), a,b son números enteros.
Manipulando el siguiente applet de Geogebra, podrás entender mejor esta casuística:
A continuación, te ofrecemos tres vídeos de operaciones con números enteros, con y sin paréntesis. Es importante que cuides la forma de operar, sé metódico y ordenado.
Importante
|
El producto de dos números enteros se obtiene ateniéndose a las reglas:
|
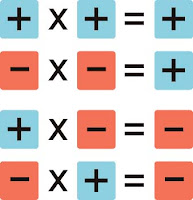 Imagen en INTEF de Antonio Ortega bajo CC |
Las operaciones con números enteros cumplen las mismas reglas que las operaciones con números naturales.
Ejemplo o ejercicio resuelto
Realiza las siguientes operaciones combinadas de números enteros:
- -3·[(2-1-7)-8]
- 2·(-8-4+12)-3·[7-(-2+1)]
Aprovecha y comprueba los resultados con la calculadora.
Las potencias. ¿Una nueva operación?
Al igual que la multiplicación es la suma de varias veces de un mismo número, la potenciación es el producto resultante de multiplicar una o varias veces ese número.
Las potencias se representan  donde
donde  es el número que se multiplica (base) y
es el número que se multiplica (base) y 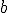 el número de veces que se hace el producto (exponente).
el número de veces que se hace el producto (exponente).
Así por ejemplo, 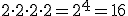 .
.
Sus propiedades son muy prácticas a la hora de simplificar cálculos:
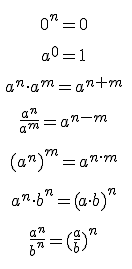
Ejemplo o ejercicio resuelto
Caso de estudio
Ejercicio 2.
Resuelve las siguientes potencias, aplicando las propiedades estudiadas en el tema:
a) 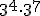 b)
b) 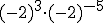 c)
c) 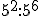 d)
d) 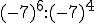 e)
e) 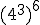
f) 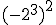 g)
g)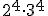 h)
h) 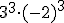 i)
i) 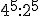 j)
j) 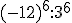
Actividad
Si observas detenidamente el ejemplo anterior podemos sacar algunas conclusiones:
- Si el signo está dentro del paréntesis, formará parte de la base y por consiguiente se repetirá tantas veces como nos indica el exponente.
- Si el signo está fuera del paréntesis, no forma parte de la base y por consiguiente se añadirá al resultado de la potencia.
- Si la base es positiva, el resultado será positivo.
- Si la base es negativa y el exponente es par, el resultado será positivo.
- Si la base es negativa y el exponente es impar, el resultado será negativo.