3. Método de Gauss

El Método de Gauss para resolver sistemas de ecuaciones lineales consiste en tomar la matriz ampliada del sistema y, mediante las transformaciones típicas de Gauss, que a continuación se enumeran, conseguir una matriz triangular superior. Hay que intentar hacer ceros todos los elementos por debajo de la diagonal principal. Una vez conseguido esto, basta volver a recomponer el sistema que queda obteniéndose un sistema escalonado, es decir, un sistema donde cada ecuación tiene una incógnita más que la anterior.

 

Recordemos, antes de empezar, los procedimientos que podemos seguir en el método de Gauss.

1. Podemos cambiar dos filas entre sí.
2. Podemos multiplicar o dividir una fila completa por cualquier número.
3. Si hay dos filas iguales podemos eliminar una de ellas.
4. Si una fila es completa de ceros, podemos eliminarla.
5. A una fila le podemos sumar (restar) otra cualquiera multiplicada por un número.

Si te fijas en concreto en la última propiedad puedes comprobar que el Método de Gauss es una generalización del Método de Reducción.

Lo mejor es que veamos, con un ejemplo, cómo se aplica el método de Gauss.

Vamos a resolver el siguiente sistema por Gauss:

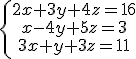
Pasamos a la matriz ampliada:

Intercambiamos lss filas 1 y 2 (nos interesa tener en la fila 1 como primer coeficiente el 1). Esto lo escribiremos como: F1 F2

Intentamos hacer ceros los elementos a₂₁ y a₃₁. Para ello, multiplicaremos la fila 1 por -2 y la sumaremos a la fila 2 y, posteriormente, multiplicaremos la fila 1 por -3 y se la sumaremos a la fila 3. Esto lo escribiremos como: F2=-2·F1+F2 ; F3=-3·F1+F3, resultando:

A continuación intentamos hacer cero el elemento que queda por debajo de la diagonal principal a₃₂. Para ello, multiplicaremos la fila 2 por 13 y la fila 3 por 11 y restaremos ambas filas. Representaremos: F3=13·F2-11·F3. Quedaría:

Ya tenemos el sistema escalonado. Procedemos de abajo hacia arriba como sigue:

54z=108 ;  z=108/54; z=2

11y-6·2=10 ; 11y=22 ; y=2

x-4·2+5·2=3 ; x=3+8-10 ; x=1

El sistema es, pues, compatible determinado.

Comprobación:

2·1+3·2+4·2=2+6+8=16

1-4·2+5·2=1-8+10=3

3·1+2+3·2=3+2+6=11

La siguiente escena de GeoGebra te puede ayudar a entender la resolución de los ejercicios que aparecen en este apartado. Mueve los deslizadores que aparecen en la parte superior de la escena para seleccionar los coeficientes de cada ecuación.

Cada ecuación se corresponde con cuatro deslizadores en sentido vertical, y los coeficientes se van seleccionando de arriba abajo, siendo el superior el de la x, el siguiente el de la y, etc. La primera ecuación se corresponde con los primeros 4 deslizadores de la izquierda.

En la parte de la derecha aparece el sistema de ecuaciones tal como va quedando a medida que vas seleccionando los coeficientes, así como la representación matricial del mismo. Cuando los hayas seleccionado todos te aparecerán abajo los sistemas equivalentes al que quieres resolver, siendo el último de la derecha el sistema escalonado.

En la parte inferior izquierda aparecen las soluciones del sistema, en el caso de que este las tenga. Los términos de sistema compatible e incompatible se explican en el apartado 3 de este tema.