3.3. División y rectificación.
DIVISIÓN
Actividad
Cuando divides una circunferencia en partes iguales estás dividiendo el
ángulo que esta comprende también en partes iguales, por tanto,
obtienes nuevos ángulos.
División de una circunferencia en partes iguales.
En este apartado aplicaremos los conceptos de bisectriz, trisección de un ángulo recto. En los procedimientos utilizaremos el compás y las plantillas de dibujo.
En todos los casos el primer paso es el dibujo de un diámetro.
- En 3, 6 y 12 partes: para dividir la circunferencia en 3 ó 6 partes iguales se necesita un diámetro. Para dividirla en 12 partes iguales tendrás que dibujar dos diámetros perpendiculares.
| División en 3 partes iguales. Vídeo de PdD alojado en Youtube | División en 6 partes iguales. Vídeo de PdD alojado en Youtube | División en 12 partes iguales. Vídeo de PdD alojado en Youtube |
Ver animación- En 4, 8 y 16 partes: para dividir la circunferencia en 4, 8 ó 16 partes iguales se necesitan dos diámetros perpendiculares. Para dividirla en 8 ó 16 partes iguales tendrás que dibujar las bisectrices a los ángulos que forman los diámetros perpendiculares.
|
- División aproximada de una circunferencia en partes iguales ( será el mismo método general para construcción de polígonos de n lados inscritos en una circunferencia ). Como su nombre indica, no es un método exacto y hay que ser muy preciso en su trazado.
Vídeo de DptoDibujoIEDA alojado en Youtube
RECTIFICACIÓN de una circunferencia
Actividad
Matemáticamente la longitud de una circunferencia se calcula aplicando la fórmula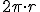 
, siendo r el radio de dicha circunferencia. Nosotros vamos a determinar esta longitud usando los utensilios de dibujo.
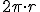, siendo r el radio de dicha circunferencia. Nosotros vamos a determinar esta longitud usando los utensilios de dibujo.
- Definición: es la obtención, mediante métodos gráficos, de un segmento equivalente a la longitud de una circunferencia, de uno de sus arcos o de una curva cualquiera. Esta longitud al estar condicionada al número
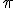es aproximada.
- Rectificación de una circunferencia: de entre todos los métodos que existen para determinar la longitud de una circunferencia nosotros optamos por el de Arquímedes. Su trazado es muy sencillo: sólo tienes que trasladar sobre una semirrecta tres veces el diámetro de la circunferencia que se quiere rectificar y una séptima parte de su diámetro.
Ejemplo: se quiere rectificar una circunferencia de diámetro 70 mm; si aplicamos el método de Arquímedes la longitud será 220 mm; (70 x 3) + (70/7) = 210 + 10 = 220.
Video de DptoDibujoIEDA alojado en Youtube
- Rectificación de una semicircunferencia. Tienes dos opciones: rectificar la circunferencia de radio igual al de la semicircunferencia dada, mediante el método anterior, y dividir la rectificación en dos partes iguales. Y la segunda realizar el siguiente procedimiento gráfico.
Video de DptoDibujoIEDA alojado en Youtube
- Rectificación de un arco de circunferencia de ángulo cualquiera. Se dan tres casos: que el ángulo sea agudo, sea recto o que sea obtuso.
En el primer caso de un arco de circunferencia de ángulo agudo tienes que aplicar el procedimiento que se explica a continuación:
Video de DptoDibujoIEDA alojado en Youtube
En el segundo (ángulo recto) tienes que aplicar el procedimiento anterior
Video de DptoDibujoIEDA alojado en Youtube
En el caso del ángulo obtuso primero debes descomponerlo en dos ángulos (uno de 90º y el otro en el resto) y rectificar ambos. Es la rectificación de un ángulo recto más un ángulo agudo.
Video de DptoDibujoIEDA alojado en Youtube
Objetivos
Arquímedes: (287 a. C. - 212 a. C.) El científico griego más importante de su época. Es considerado uno de los matemáticos más grandes de la historia, además de físico astrónomo, ingeniero e inventor.