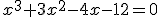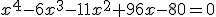2.1. Ecuaciones polinómicas de grado superior a dos

Actividad

Antes de explicar como se resuelven ecuaciones de este tipo, recuerda que la división por el método de Ruffini ha sido explicada en el tema anterior.

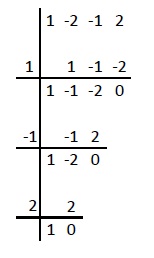Las ecuaciones polinómicas son de la forma P(x)=0 donde P(x) representa un polinomio de cualquier grado. Teniendo en cuenta esto, las soluciones de la ecuación coinciden con las raíces del polinomio. Por tanto, para resolver la ecuación se factoriza el polinomio y se calculan sus raíces.

Veamos, por ejemplo, la siguiente ecuación:

Las posibles raíces enteras del polinomio coincidían con los divisores del término independiente, por tanto aplicamos la regla de ruffini probando con los divisores del 2: 1, -1, 2 y -2

De esta forma las raíces que salen son 1, -1 y 2 que son las soluciones de la ecuación de partida.

Actividad

En ecuaciones como la anterior no es necesario aplicar Ruffini hasta encontrar las tres raíces.

Cuando aplicamos Ruffini y llegamos a un polinomio de 2.º grado como cociente, lo transformamos en ecuación de segundo grado que podemos resolver y obtener las dos soluciones restantes.

En el ejemplo anterior:

Aplicamos Ruffini y encontramos la primera solución que sería 1:

El cociente resultante de dicha división sería la ecuación de 2.º grado x²-x-2=0, de manera que si resolvemos esta ecuación obtenemos de forma sencilla las otras dos soluciones:

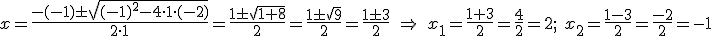
$x=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot{1\cdot{(-2)}}}}{2\cdot{1}}=\frac{1\pm\sqrt{1+8}}{2}=\frac{1\pm\sqrt{9}}{2}=\frac{1\pm3}{2}\Rightarrow{x_1=\frac{1+3}{2}=\frac{4}{2}=2};x_2=\frac{1-3}{2}=\frac{-2}{2}=-1$