3.2. Ejercicios de representación gráfica de parábolas

Importante

Imagen en Flickr de Artemedion bajo CC

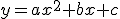El proceso a seguir para la representación de una función en la forma y=ax^2+bx+c

es el siguiente.

Cálculo del eje.
El eje de la parábola nos la da la expresión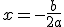 $x=-\frac{b}{2a}$ .

Cálculo del vértice.
La abscisa del vértice ya la tenemos pues es el valor anterior, para hallar la otra componente basta sustituir en la función y hallar su valor.

Cálculo de otros puntos.
Una vez fijado el vértice, sólo nos falta saber cómo se comporta la función en puntos cercanos a él. Lo usual es hallar los puntos de corte con los ejes ya que esos puntos nos dan mucha información. Para hacer esto se procede de la siguiente forma:

Puntos de corte con el eje X.
Resolvemos la ecuación ax^2+bx+c=0
Las soluciones que obtenemos son las abscisas de los puntos de corte con el eje X.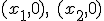

Puntos de corte con el eje Y.
Hacemos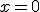 en la función 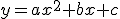y obtenemos . Por tanto el punto de corte con eje Y es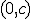

En el caso de que tengamos la función en la forma 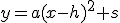y=a(x-h)^2+s los pasos que daremos para hallar la representación gráfica son idénticos a los mencionados más arriba. No obstante, aquí podemos obtener directamente el vértice de la parábola 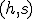(h,s) lo cual junto al signo del coeficiente a ya nos puede permitir crear un esbozo de la forma de la misma.

Actividad de rellenar huecos

Imagen en Flickr de visualpanic bajo CC

Nuestro amigo Esteban está juntando dinero para comprarse un iPod. De pronto aparece una oferta y quiere aprovecharla, pero al hacer recuento observa que le faltan 100 euros. Consigue que su padre se los preste con el compromiso de devolvérselos. Como al principio va a tener más problemas hasta que empiece a ahorrar, le propone a su padre darle 1 euro la primera semana, 3 la segunda, 5 la tercera y así sucesivamente hasta condonar la deuda.

Rellena la siguiente tabla colocando en cada celda lo que ha entregado hasta ese momento a su padre, para así saber cuándo ha cubierto la deuda completa.

Atención: en la tabla no debes colocar lo que entrega cada semana sino lo que ha entregado en total a su padre hasta ese momento.

nº de semana	1	2	3	4	5	6	7	8	9	10
entregado hasta el momento	Rellenar huecos (1): JXUwMDY5	Rellenar huecos (2): JXUwMDZj	Rellenar huecos (3): JXUwMDYx	Rellenar huecos (4): JXUwMDY5JXUwMDA3	Rellenar huecos (5): JXUwMDZhJXUwMDA3	Rellenar huecos (6): JXUwMDZiJXUwMDA1	Rellenar huecos (7): JXUwMDZjJXUwMDBk	Rellenar huecos (8): JXUwMDZlJXUwMDAy	Rellenar huecos (9): JXUwMDYwJXUwMDA5	Rellenar huecos (10): JXUwMDY5JXUwMDAxJXUwMDAw

Enable JavaScript

Si los valores que has obtenido en la tabla anterior los representamos en unos ejes de coordenadas, obtenemos la siguiente gráfica. La línea discontinua no tendría sentido dibujarla en este caso, sólo lo hacemos para que veas cuál es la evolución real de los valores de la función.

Fuente propia realizada con GeoGebra bajo Dominio público

Como ves por la tabla o la gráfica, a cada valor le corresponde precisamente su cuadrado. En este caso podemos encontrar fácilmente su expresión algebraica que sería 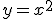y=x^2 .

Reflexión

Imagen en Flickr de titoalfredo bajo CC

En una empresa que fabrica alfombras, tienen un determinado diseño que solo fabrican en alfombras cuadradas. Pueden realizar una alfombra de cualquier medida, pero siempre cuadrada. Escribe la función que relaciona la medida del lado de la alfombra con la superficie que va a cubrir esa alfombra.

Importante

Completa los espacios en blanco indicando qué número de gráfica corresponde a cada expresión analítica.

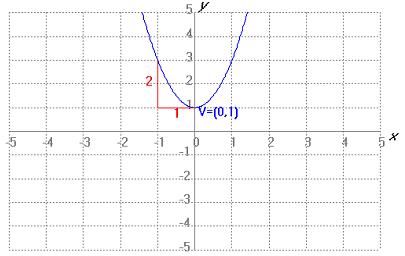
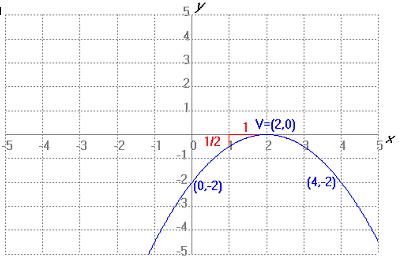
Fuente propia con GeoGebra bajo Dominio público	Fuente propia con GeoGebra bajo Dominio público
Gráfica 1	Gráfica 2
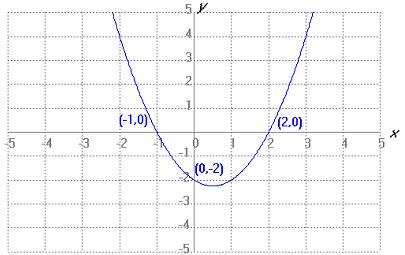
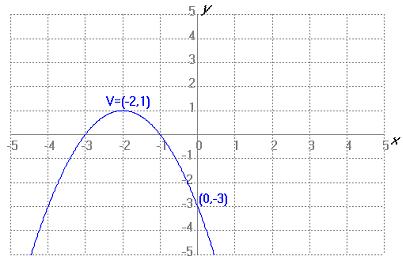
Fuente propia con GeoGebra bajo Dominio público	Fuente propia con GeoGebra bajo Dominio público
Gráfica 3	Gráfica 4

AV - Reflexión

Explica de forma razonada cómo has resuelto la actividad anterior.

Retroalimentación

Las gráficas 1 y 3 corresponden a parábolas abiertas hacia arriba, es decir, el coeficiente de la x^2 en sus expresiones analíticas es positivo.

La gráfica 1 corta al eje de ordenadas en el punto (0,1) , tiene el vértice en el punto (0,1) , no corta al eje OX, es simétrica respecto del eje OY, y al desplazarnos una unidad desde el vértice hacia la derecha o hacia la izquierda subimos 2. Resulta de desplazar la parábola y=2x^2 verticalmente una unidad hacia arriba. Corresponde a la función b) y=2x^2 +1

La gráfica 3 corta al eje de ordenadas en el punto (0,-2) y al eje OX en los puntos $(-1,0)\begin{verbatim} y \end{verbatim}(2,0)$ , corresponde a una parábola del tipo $y=a \cdot (x-x_1) \cdot (x-x_2)$ donde x_1 y x_2 son los valores de la en los puntos de corte con el eje de abscisas. Es decir es de la forma como pasa por el punto (0,-2) tenemos que

Por tanto, a la función y= (x+1)(x-2) que corresponde con la opción d)

Las gráficas 2 y 4 corresponden a parábolas abiertas hacia abajo, es decir el coeficiente de la x^2 en sus expresiones analíticas es negativo.

La gráfica 2, corta al eje de ordenadas en el punto (0,-2) , tiene el vértice en el punto (2,0) , corta al eje OX, en el punto (2,0) , es simétrica respecto de la recta x= 2 , y pasa por el punto (4,-2) . Como conocemos tres puntos de la parábola podemos generar un sistema de tres ecuaciones al introducir las coordenadas de los puntos en la expresión de la parábola y=ax^2+bx+c

$\left. \begin{eqnarray} (0,-2) & \Rightarrow & a \cdot (0)^2 + b \cdot (0) +c & = & -2 \\ (2,0) & \Rightarrow & a \cdot (2)^2 + b \cdot (2) +c & = & 0 \\ (4,-2) & \Rightarrow & a \cdot (4)^2 + b \cdot (4) +c & = & -2 \end{eqnarray} \right\} \Rightarrow \left. \begin{eqnarray} c & = & -2 \\ 4a + 2b +c & = & 0 \\ 16a + 4b+c & = & -2 \end{eqnarray} \right\}$

De la primera igualdad obtenemos que c= -2 .

Si sustituimos el valor de en las otras dos igualdades, tenemos que

$\left\{ \begin{eqnarray} 4a + 2b -2 & = & 0 \\ 16a + 4b-2 & = & -2 \end{eqnarray} \right.$

Al resolver este sistemos obtenemos los valores de $a=-\frac{1}{2}, \ b=2, \ c=-2$ con lo que la función correspondería con la opción a.

$y = -\frac{1}{2}x^2+2x-2 = -\frac{1}{2} $x2-4x+4$ = -\frac{1}{2} (x-2)^2.$

La gráfica 4 corta al eje de ordenadas en el punto (0,-3) y tiene el vértice en el punto (-2,1) .

Conociendo el vértice y un punto (distinto de él) por el que pase, utilizamos la fórmula y=a(x-x_v)^2+y_v siendo x_v e y_v y calculamos a sustituyendo las coordenadas del mismo.

Es decir, la ecuación de la parábola es y=a(x+2)^2+1 y como pasa por (0,-3) tenemos que

$-3=a((0)+2)^2+1 \ \Rightarrow \ -3=4a+1 \ \Rightarrow \ a= -1$

Luego corresponde a la función c) y= -(x+2)^2+1 = -x^2 -4x -3

Caso de estudio

Imagen enFlickr de Alessandro Zilio bajo CC

Antonio, uno de los empleados de TRANS VELOX en Córdoba, tiene una pequeña discoteca en el centro de la ciudad.

Un día que estuvo en la caseta, invitó al gerente a que se llegara por la noche.

La discoteca abre sus puertas a las nueve de la noche, sin ningún cliente, y las cierra cuando se han marchado todos.

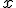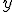Llamamos al número de horas que está abierta la discoteca e al número de clientes que hay en cada momento. Suponemos que la expresión analítica que relaciona al número de clientes con el número de horas que lleva abierta la discoteca es:

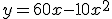
¿Cuántos clientes tiene a las 10 de la noche? ¿Y a las 12?
¿A qué horas hay en la discoteca 80 personas?
Dibuja la gráfica correspondiente a la expresión anterior.
Determina el número máximo de clientes que van un sábado por la noche a la discoteca y a qué hora ocurre.
Un sábado que estuvo Ignacio había menos de 80 personas y más de 50. ¿A qué hora estuvo?
¿A qué hora cierra Antonio?

Retroalimentación

Si Antonio abre a las nueve de la noche, a las diez ha pasado una hora y el número de clientes será $y=60 \cdot 1-10 \cdot 1^2 =50$ A las 12 de la noche el número de clientes será $y=60 \cdot 3-10 \cdot 32 =90$ .

En la discoteca habrá 80 personas a las 11 de la noche y a la 1 de la madrugada ya que si resolvemos la ecuación de segundo grado que resulta de la igualdad obtenemos es decir, a las 2 y a las 4 horas después de abrir la discoteca.

La gráfica es una parábola con las ramas hacia abajo ya que el coeficiente de es negativo. Tiene el vértice en el punto $(3, \ 60 \cdot 3-10 \cdot 32)=(3, \ 90),$ porque es el punto medio de $x=0\begin{verbatim} y \end{verbatim}x=6$ que son los puntos de corte con el eje OX, ya que son las soluciones de la ecuación de segundo grado

Fuente propia realizada con geogebra bajo Dominio público

El número máximo de clientes es 90 y esto ocurre 3 horas después de abrir, es decir, a las 12 de la noche.

Si el sábado que estuvo Ignacio había más de 50 personas y menos de 80, tuvo que ir entre las 10 y las 11 de la noche, o bien entre la 1 y las 2 de la madrugada.

La hora de cierre será cuando se hayan ido todos los clientes, es decir, 6 horas después de abrir, a las 3 de la madrugada.

Caso de estudio

Vamos a considerar una de las funciones que viste en el apartado anterior que tuviese por ejemplo un coeficiente 2 multiplicando al cuadrado, como eje la recta 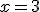x=3 y estuviese desplazada hacia arriba 4 unidades. La expresión que vimos era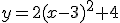

Utiliza los conocimientos adquiridos anterioemente y opera esa expresión para obtener una expresión más simplificada.

Reflexión

Representa la función

realizando el estudio previo de los valores importantes.

Caso de estudio

Imagen en Flickr de Sauce Babilonia bajo CC

El dueño de una papelería ha recibido una remesa de bolígrafos dedicados a la serie de televisión El Internado. Sabe que si los vende a 3 euros puede vender unos 20 ejemplares a la semana. Para ganar más dinero decide subir los precios pero observa que por cada 50 céntimos más que aumente el precio vende dos bolígrafos menos.

¿Cuál sería la función que relaciona el número de veces que sube el precio con el dinero que recauda por la venta? Representa gráficamente la función.

Reflexión

A la vista de la gráfica que has representado en el apartado anterior, ¿cuál es el precio que debe poner a los bolígrafos para obtener el máximo beneficio? ¿Cuál será ese beneficio máximo?