2.1. Circunferencia

Imagen en Flickr de Fersanam bajo CC

Llamamos circunferencia al lugar geométrico de los puntos de un plano tales que equidistan de un punto fijo llamado centro. La forma tradicional de trazar una circunferencia en la antiguedad era marcar el centro de la misma, y en este atar un cordel de una longitud determinada en cuyo extremo había un punzón o cualquier tipo de instrumento que marque el recorrido. Al girar el cordel el punzón describía esta figura geométrica como se muestra en la siguiente escena de geogebra si pulsas sobre el botón situado en la parte inferior izquierda de la misma.

Fuente propia bajo Dominio público

Si no puedes ver la anterior escena accede a la siguiente página.

Importante

Para deducir la ecuación de la circunferencia, expresamos analíticamente la condición:

$\begin{verbatim}d\end{verbatim} (P,C) =\sqrt{(x-a)^2 + (y-b)^2} = r \Rightarrow (x-a)^2 + (y-b)^2 = r^2$

Siendo a y b las coordenadas del centro de la circunferencia. Si desarrollamos la anterior ecuación obtenemos la ecuación general de la circunferencia que es la siguiente:

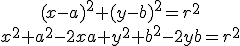
$(x-a)^2 + (y-b)^2 = r^2 \\ x^2+a^2 -2xa + y^2 +b^2 - 2yb = r^2 \\$

Si llamamos 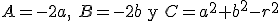$A=-2a, \ B=-2b \begin{verbatim}y\end{verbatim} C= a^2+b^2-r^2$ obtenemos la ecuación general de la circunferencia

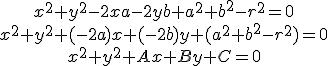
$\begin{array}{c}x^2+ y^2 -2xa - 2yb + a^2 + b^2 - r^2 = 0 \\ x^2+ y^2 +(-2a)x +(-2b)y + (a^2 + b^2 - r^2) = 0 \\ x^2+ y^2 +Ax +By + C = 0 \end{array}$

Si el centro C coincide con el origen de coordenadas, se tiene que 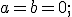la ecuación resultante, conocida como la ecuación reducida de la circunferencia, es la siguiente:

En la aplicación de GeoGebra de más abajo se pueden modificar los valores de a, b y r a través de las barras de deslizamiento de dichos parámetros. Para ello pon el cursor del ratón en los puntos de las barras de deslizamiento, haz clic con el botón izquierdo y manteniendo pulsado el mismo, al mover el ratón cambiarán los valores de a, b y r y verás cómo cambia la forma y posición de la circunferencia así como las ecuaciones que la representan.

Fuente propia bajo Dominio público

Caso de estudio

Halla la ecuación de la circunferencia centrada en el origen y que pasa por el punto (2,2).

Caso de estudio

Halla la ecuación de una circunferencia sabiendo que uno de sus diámetros tiene por extremos los puntos A(-6,4) y B(-6,8).

Retroalimentación

La siguiente imagen ilustra el planteamiento del problema.

Fuente propia realizada con geogebra bajo Dominio público

Para resolverlo necesitamos dos datos:

El radio de la circunferencia.
Este viene dado por la distancia entre los puntos A y B dividido entre 2 ya que el enunciado nos dice que ambos son extremos del diámetro de la circunferencia.

$\begin{array}{c} \begin{verbatim}d\end{verbatim}(A,B)=\sqrt{(-6-(-6))^2+(8-4)^2}=4 \ \Rightarrow r=\frac{\begin{verbatim}d\end{verbatim}(A,B)}2=\frac{4}{2}=2 \ \begin{verbatim}unidades\end{verbatim} \end{array}$

Las coordenadas del centro.
Para hallar estas coordenadas tenemos que utilizar las fórmulas que nos dan las coordenadas del punto medio de un segmento conociendo las coordenadas de los extremos.

Si tenemos un segmento de extremos $A(x_1,y_1) \begin{verbatim} y \end{verbatim} B(x_2,y_2)$ , las coordenadas del punto medio son:

$x_0=\frac{x_1+x_2}{2} \\ y_0=\frac{y_1+y_2}{2}$

Para nuestro caso tenemos que $A(-6,4) \begin{verbatim} y \end{verbatim} B(-6,8)$ por tanto

$\left. \begin{array}{l} x_0=\frac{-6-6}{2}=-\frac{12}{2}=-6\\ y_0=\frac{4+8}2=\frac{12}2=6 \end{array} \ \ \right} \ M=(-6,6)$

Una vez conocido el centro (-6, 6)

y el radio la circunferencia 2, la ecuación de la misma será:

$\begin{array}{c} (x-(-6))^2+(y-(6))^2=(2)^2 \\ (x+6)^2+(y-6)^2=4 \end{array}$

Y la ecuación general será:

Caso de estudio

Halla la ecuación de la circunferencia de centro C(1,-1) que pasa por el punto P(3,3). Halla los puntos de corte de dicha circunferencia con el eje de abscisas.