4.2. Asíntotas horizontales
Importante
La función f(x) tiene una asíntota horizontal en y = b si se cumplen una de estas dos condiciones
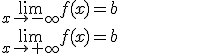
Importante
Límites de funciones polinómicas
El problema de calcular el límite de una función polinómica cuando x tiende a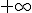 
ó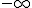 
, puede verse reducido al cálculo del límite del término de mayor grado, ya que el resto de términos tiene un crecimiento muy inferior comparado con el de grado mayor.
Así, calcular el límite de la función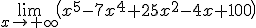 
es análogo a calcular el límite de 
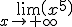, por lo que el límite de ambas funciones es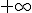
Límites de funciones racionales
Por lo tanto, el cálculo de los límites de las funciones racionales se puede reducir con la siguiente expresión.
Límite de una función racional si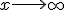 
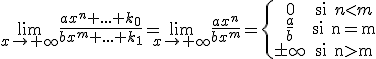
En caso de existir en el numerador o en el denominador una expresión de la forma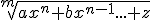 
el crecimiento de la función es análogo a 
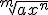cuando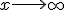
Caso práctico
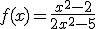
Caso práctico
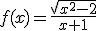
Caso práctico
En el applet siguiente tiene representada una función racional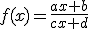 
cuyos coeficientes puedes modificar con los deslizadores de la izquierda (siempre debe ser 
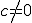pues si no se convertiría en una recta). Puedes ver que posee dos asíntotas una vertical y otra horizontal.