4.1. Asíntotas verticales
Importante
Una función f(x) tiene una asíntota vertical en x = a si
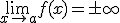
Ejemplo:
Calculemos las asíntotas verticales de la función 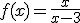
El denominador de la función, x-3 se anula para el valor x=3. Para ello, tan solo debemos resolver la ecuación x-3 = 0 para determinar la solución, x = 3.
Si calculamos los límites de la función en x= 3 llegamos a los siguientes resultados
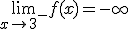
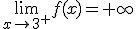
Podemos afirmar que la función 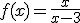 tiene una asíntota vertical en x = 3
tiene una asíntota vertical en x = 3
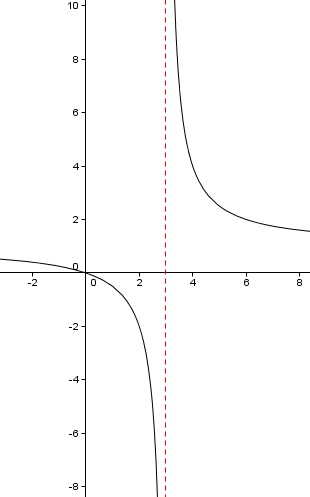
Observa la gráfica de la función, que esta a la derecha.
Caso práctico
Determina las asíntotas verticales de la función 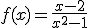
Comprueba lo aprendido
Nos podemos preguntar si toda función racional tiene asíntotas verticales. La respuesta es no y veremos un caso para confirmar esta afirmación.
Calculemos las asíntotas de la función 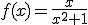 .
.
Para ello, tan solo calculamos las soluciones de la ecuación x2+1=0
Las soluciones de dicha ecuación serán 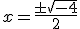 . Al no existir la raiz de -4, la ecuación no tiene soluciones y, por supuesto, la función no tiene asíntotas.
. Al no existir la raiz de -4, la ecuación no tiene soluciones y, por supuesto, la función no tiene asíntotas.
Comprueba lo aprendido
Retroalimentación
Falso
x= -1 no puede ser solución de la función indicada, ya que la única solución de 1-x =0 es x=1