3.2. Discontinuidades y sus tipos
En el apartado anterior, hemos visto que se deben cumplir una serie de condiciones para que una función sea continua. Por lo tanto, si no se cumple alguna, diremos que la función es discontinua. Ahora estudiaremos que existen varios tipos de discontinuidades.
Importante
Una discontinuidad se dice evitable en x= a si existe el límite de la función en el punto y es finito, pero no coincide con el valor f(a) o no existe dicho valor.
La discontinuidad se llama de tipo evitable, ya que podemos "evitar la discontinuidad" si definimos 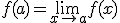
Ejemplo:
Veamos un caso concreto, la función definida como
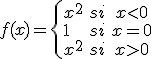
Esta función, para el valor x = 0, verifica que f(0) = 1 tal y como hemos definido la función, sin embargo, 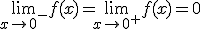 . Por lo tanto , la función presenta una discontinuidad evitable tal y como podemos ver en su representación, ya que si definimos f(0) = 0, la función sería continua.
. Por lo tanto , la función presenta una discontinuidad evitable tal y como podemos ver en su representación, ya que si definimos f(0) = 0, la función sería continua.
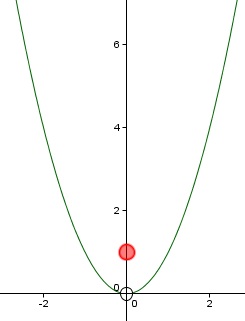
Puedes ver lo que ocurre en la gráfica de la función:
Importante
Una función presenta una discontinuidad en x= a de salto o de primera especie si existen los límites laterales y son distintos o al menos uno de ellos es infinito.
Se dirá que la discontinuidad es de salto finito si los límites laterales son finitos y de salto infinito si al menos uno de ellos es infinito.
Ejemplos:
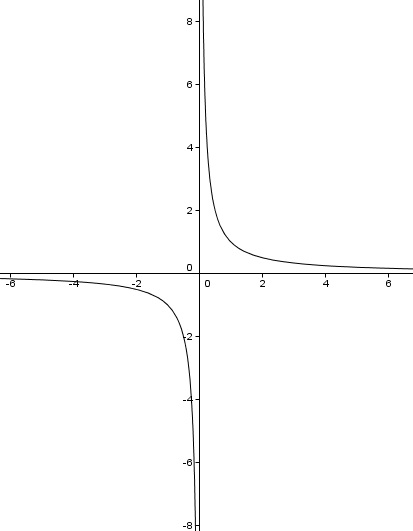
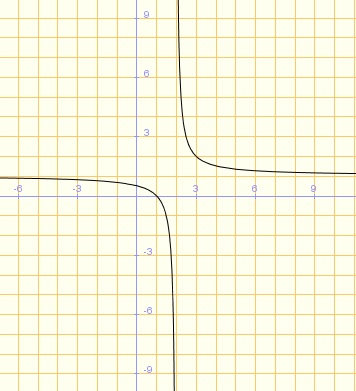
Un ejemplo muy visual de función con una discontinuidad de primera especie en x= 0 y en particular de salto infinito es 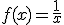 , ya que al estudiar los límites laterales en el punto x= 0 obtenemos:
, ya que al estudiar los límites laterales en el punto x= 0 obtenemos:
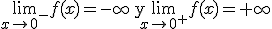
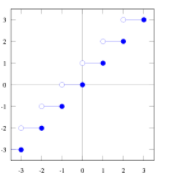
Si tomamos la función f(x) = Ent(x), es decir la parte de entera de un número detectamos que dicha función tiene una discontinuidad de 1º especie, de salto finito en los números enteros. Estudiemos, por ejemplo, la discontinuidad en x= 1
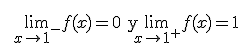
Caso práctico
Estudia la continuidad de la siguiente función f(x) e indica, si existe, su tipo de discontinuidad.
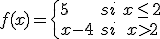
Caso práctico
Estudia el tipo de función y discontinuidad de : 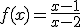
Para saber más
En el siguiente vídeo repasamos los tipos de discontinuidad que hemos visto.
Vídeo de estudiia alojado en Youtube