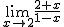3.1. Continuidad de una función
En este video puedes apreciar la idea de función continua. Como hemos indicado anteriormente, simplemente diremos que es continua si podemos dibujarla sin levantar el lápiz del papel. En este video puedes visualizar esta explicación.
Vídeo de Alberto Adones Aranda alojado en Youtube
Gráficamente, es muy sencillo determinar si una función es continua, ahora veremos cómo determinar si una función dada analíticamente es continua.
Importante
Una función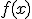 
se dice continua en un punto 
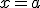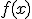, si se aproxima a 
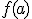cuando 
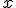se acerca a 
, o lo que es lo mismo, si cumple las siguientes tres condiciones:
1. Que exista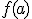
2. Que exista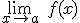 
3. Que los dos valores anteriores coincidan, es decir,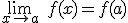 
En caso contrario, la función se dirá discontinua en dicho punto.
Una función que es continua en todos los puntos donde está definida, se dirá continua.
Importante
Podemos indicar algunos criterios de continuidad en función del tipo de función
Las funciones polinómicas son continuas en todo el conjunto de los números reales.
Las funciones racionales son continuas en todos los números reales, salvo en aquellos puntos donde se anule el denominador.
Las funciones potenciales, exponenciales y logarítmicas son continuas en todo su dominio de definición.
Ejemplo:
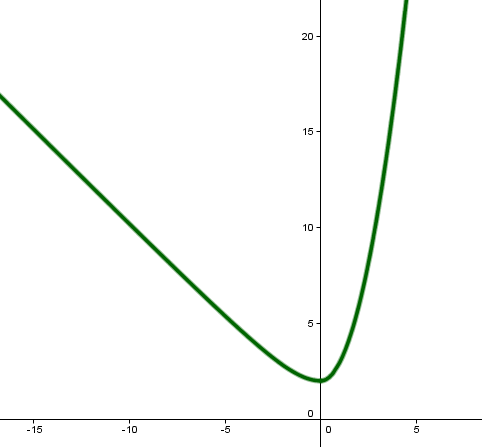Veamos un caso concreto del estudio de una función definida a trozos y analicemos la continuidad de la función
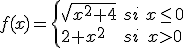
La función para x< 0 es continua ya que estamos ante una raíz cuadrada de un radicando siempre positivo (x2 + 4 siempre es positivo) por lo que siempre existe el resultado de dicha raíz. Si x>0 nos encontramos antes un polinomio, por lo que es continua en todo el intervalo. Tan solo debemos comprobar si la función es continua en 0
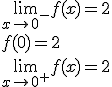
Vemos que los dos límites laterales coinciden y además su resultado es igual al valor de la función en ese punto. Por lo tanto la función es continua en todos los números reales.
Caso práctico
 |
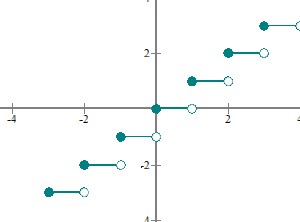La función que está en la imagen de la izquierda, como ya sabes, es la parte entera y=Ent(x).
Estudiemos la continuidad en los números enteros. Cojamos por ejemplo x=2. Si nos acercamos a 2 por la izquierda como sigue
| x | 1,9 | 1,99 | 1,999 | 1,9999 | 1,99999 |
| Ent(x) | 1 | 1 | 1 | 1 | 1 |
o sea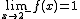 
, como se ve en el dibujo de la función nos acercamos a 1 pero no llegamos (punto hueco)
| x | 2,001 | 2,0001 | 2,00001 | 2,000001 |
| Ent(x) | 2 | 2 | 2 | 2 |
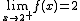; Los límites laterales no coinciden, por tanto, la función no es continua en x=2.
La parte entera es discontinua de salto finito en los enteros.
Comprueba lo aprendido
Retroalimentación
Verdadero
La función lineal es continua siempre y en concreto en el punto 1.Retroalimentación
Falso
Los límites laterales de la función en x=1 tienden a más y menos infinito, por lo que no existe valor real del límite y la función no es continua.Retroalimentación
Verdadero
Sí es continua ya que su límite vale 2 que coincide con f(1).Comprueba lo aprendido
Vamos a estudiar la continuidad de la función que aparece representada en la imagen.
Imagen de elaboración propia
Para ello completa las siguientes frases:
Importante
Recordamos la definición que hemos visto de continuidad: f es continua en a si 
Esto facilita muchísimo el límite de una función en punto para las funciones continuas en todo su dominio, que, como hemos visto, son la mayoría de las funciones elementales.
Calcular el límite de f(x)=x3+4x+7 cuando x tiende, por ejemplo, al punto -1, es muy fácil. Como f(x) es una función polinómica, por tanto continua en todo su dominio, basta con hallar f(-1).
Caso práctico
a)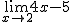 
b)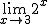 
c)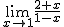 
d) 