3. Sistemas de ecuaciones lineales
 Imagen propia bajo Dominio público
|
Ya hemos visto en el apartado anterior el concepto de ecuación lineal. Formalmente, llamamos ecuación lineal con dos incógnitas a una ecuación del tipo: 
, donde 
y 
son números reales cualesquiera, este tipo de ecuaciones tienen infinitas soluciones, veamos un ejemplo:
 |
Para hallar algunas de las soluciones de esta ecuación despejamos la y.
 |
Posteriormente le damos a la x una serie de valores cualesquiera y hallamos el valor de la y correspondiente; por ejemplo si la x=0 entonces: 
, los resultados que vamos obteniendo los podemos ordenar en una tabla como la siguiente:
| x | y |
| 0 | 3 |
| 1 | 1 |
| 2 | -1 |
| 3 | -3 |
| 4 | -5 |
Todas las soluciones anteriores verifican la ecuación de arriba, es decir; si sustituimos la x y la y de la ecuación por cada uno de los pares de valores que aparecen en la tabla vemos que se verifica en todos ellos la igualdad, como se puede apreciar en la siguiente tabla.
| x=0, y=3 | 2·0+3=3 |
| x=1, y=1 | 2·1+=3 |
| x=2, y=-1 | 2·2-1=3 |
| x=3, y=-3 | 2·3-3=3 |
| x=4, y=-5 | 2·4-5=3 |
Llamamos sistema de dos ecuaciones lineales con dos incógnitas a una expresión algebraica de este tipo:
 |
siendo x e y las incógnitas del sistema de ecuaciones, cuyo valor hay que hallar, 
números reales conocidos como "coeficientes de la ecuación" y 
términos independientes.
Los sistemas de ecuaciones tienen su aplicación en una gran diversidad de situaciones y contextos como podrás apreciar en apartados posteriores de este mismo tema.
Un ejemplo concreto de sistemas de este tipo puede ser el siguiente.
 |
Solucionar un sistema como el anterior significa hallar, si existe, una solución común, a las dos ecuaciones lineales con dos incógnitas que lo forman. Como en el ejemplo de arriba podemos hallar algunas de las soluciones de cada una de las ecuaciones y recogerlas en una tabla como hemos hecho en el caso anterior.
|
|
 |
||||||||||||||||||||||||
|
|
 |
||||||||||||||||||||||||
|
|
Hemos marcado en negrita las dos soluciones comunes a ambas ecuaciones, esta es la solución del sistema: x=2, e y=-1. Esto lo podemos comprobar sustituyendo la "x" y la "y" en cada una de las ecuaciones y viendo que se verifican de forma simultánea ambas.
 |
Existen distintos métodos que nos permiten llegar a conocer estas soluciones: método de sustitución, igualación y reducción.
Dado el siguiente sistema de dos ecuaciones con dos incógnitas.
 |
La solución de dicho sistema es x=2 e y=2. Si sustituimos en las ecuaciones de arriba las incógnitas por el valor de las soluciones vemos que se cumplen las igualdades.
 |
Caso de estudio
Comprueba que 
e 
es solución del siguiente sistema.
|
Pregunta Verdadero-Falso
Retroalimentación
Verdadero
Retroalimentación
Falso
Retroalimentación
Verdadero
Importante
Llamamos sistema de tres ecuaciones lineales con tres incógnitas a un sistema que adopta la siguiente forma:
 |
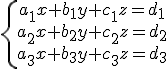Donde x, y, z son las incógnitas a resolver y los coeficientes que multiplican a las mismas números reales cualesquiera.Como en el caso de los sistemas de dos ecuaciones con dos incógnitas resolver un sistema de tres ecuaciones con tres incógnitas consiste en hallar los valores de x, y, z, en el caso de que existan, que cumplen las igualdades anteriores, por ejemplo la solución del siguiente sistema.
 |
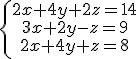Es: x=7, y=-3, z=6 ya que se verifica que:
 |
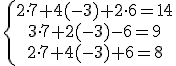Veamos otro ejemplo:
 |
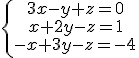Los valores x=1, y=-3, z=-6 conforman una solución del sistema anterior ya que se cumple:
 |
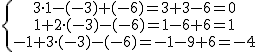Igualmente que en el caso de sistemas de ecuaciones lineales con dos incógnitas, podríamos utilizar los métodos de sustitución, igualación y reducción para resolver sistemas de tres ecuaciones con 3 incógnitas. En el próximo tema aprendermos a resolver sistemas de ecuaciones lineales de una forma diferente, mediante matrices, siguiendo el método de Gauss.
Importante
Para que un sistema de ecuaciones tenga una única solución deberemos tener al menos tantas ecuaciones como incógnitas.
Por tanto si planteamos problemas con tres incógnitas, deberemos obtener tres ecuaciones para encontrar su única solución.
Para saber más
Breve historia de los sistemas de ecuaciones
Según informaciones extraidas del Papiro de Rhind que se remonta al 1650 a. c. Los egipcios yan conocian ecuaciones lineales del tipo 
y 
. En mesopotamia ya aparecen problemas más complejos. Así en un texto babilónico aparece un sistema de dos ecuaciones lineales con dos incógnitas llamadas respectivamente "el primer anillo de plata" y "el segundo anillo de plata". Dicha ecuación modernamente adoptaría la siguiente forma:
 |
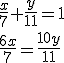Sistemas como el anterior en ocasiones lo resolvían los babilonios por un método parecido al de reducción así si multiplicamos la primera ecuación por 6 obtenemos el siguiente sistema:
 |
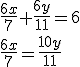A continuación si a la primera ecuación se le resta la segunda obtenemos la siguiente ecuación:
 |
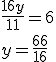Conociendo el valor de la y podemos hallar el valor de la x a partir de la segunda ecuación del sistema:
 |
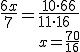En otras civilizaciones, como la china, encontramos referencias a sistemas de ecuaciones y sus métodos de resolución. Así en el libro Chui-chang, suan-shu (Nueve capítulos sobre el arte matemático) escrito en el año 250 a. C. aparece el siguiente sistema de ecuaciones:
 |
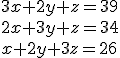El autor lo resuelve utilizando un procedimiento de sumas y restas de los coeficientes de las incógnitas que le permite obtener un sistema equivalente al anterior (con las mismas soluciones) pero escalonado.
 |
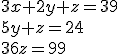Del cual pueden obtenerse fácilmente, y de una manera sucesiva, los valores de x, y, z. Estos son: 
. Este método de resolución aparecería en occidente unos 1.500 años después y sería conocido como el método de Gauss, que ya has visto en este tema. Como ejercicio puedes comprobar que ambos sistemas tienen como solución los valores de x, y, z indicados arriba.