3.4. Clasificación de los sistemas de ecuaciones lineales en función del número de soluciones
Importante
Un sistema de ecuaciones lineales se dice que es compatible si tiene solución y en caso contrario se llama incompatible.
Si el sistema es compatible y tiene una única solución recibe el nombre de compatible determinado. Y si tiene infinitas soluciones se llama compatible indeterminado.
Esta clasificación podemos resumirla en el siguiente esquema.
 |
Por ejemplo. El siguiente sistema de ecuaciones:
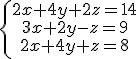 |
Cuya solución es: x=7, y=-3, z=6 es compatible determinado ya que presenta una única solución según el anterior esquema.
Veamos otros ejemplos:
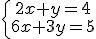 |
El sistema no tiene solución por lo que es incompatible.
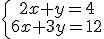 |
En este otro caso el sistema presenta infinitas soluciones por lo que lo llamamos compatible indeterminado.
Para comprobar la compatibilidad e incompatibilidad de un sistema de ecuaciones hemos de resolverlo antes por cualquier método, la existencia o no de solución nos determinará la clase de sistema ante el cual nos encontramos.
En el tema siguiente encontrarás una estrategia para poder clasificar un sistema de ecuaciones sin necesidad de resolverlo.