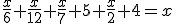2. Ecuaciones
 |
|
Planet, de Southernpixel, |
¿Sirven las ecuaciones en el mundo que nos rodea?
Ya sea consciente o inconscientemente, resolvemos problemas del día a día por medio de ecuaciones: al comparar productos en el mercado, cuando hacemos viajes, en nuestras cuentas bancarias y al buscar una nueva compañía telefónica. Incluso para hacer la foto de la izquierda, se han usado ecuaciones.
 |
| X de hidden side, CC by-nc-sa 2.0 |
Hay muchas situaciones en las que necesitamos hallar cantidades desconocidas a partir de una serie de datos. Cada cantidad que no conozcamos va a ser una incógnita.
Se suele decir que las matemáticas nos rodean, y en el caso de las ecuaciones es muy cierto. Por ejemplo, para que un aparato de GPS pueda determinar tu posición (incógnita), éste obtiene datos de al menos tres satélites con los que plantea una serie de ecuaciones que determinan la solución. Otro ejemplo, al programar el termostato del aire acondicionado ¿cuándo debe apagarse y encenderse el equipo para que la temperatura esté según lo deseado? Más ecuaciones...
Aunque a veces oímos hablar de ecuaciones con una incógnita, lo cierto es que en un problema puedes encontrarte con varios datos desconocidos. También veremos que un mismo problema puede tener una, dos soluciones, o puede que ninguna ¡Incluso es posible que tenga infinitas soluciones! ¿Pero sabes exactamente qué es una ecuación? Vamos a dar una definición.
Una ecuación es una expresión algebraica en la que establecemos una igualdad. El signo igual separa la ecuación en dos miembros. Como es una expresión algebraica, estará formada por números, variables y operaciones. En el caso de las ecuaciones, a las variables las llamaremos incógnitas, pues son los valores que queremos descubrir.
Podemos clasificar las ecuaciones en función del número de incógnitas.
Ejemplos:
Ecuación con una incógnita: 2+x=8
Ecuación con dos incógnitas: 2x+3y=6
Ecuación con tres incógnitas: x+3y-2z=6
Y así podríamos continuar.
Iguamente podríamos hacer una clasificación de las ecuaciones en función del grado de la variable:
Ejemplos:
Ecuación de primer grado: x+3=2x-5
Ecuación de segundo grado:x 2-5x=6
Ecuación de tercer grado: x-2x3=8x2+3
Y así sucesivamente.
Las ecuaciones se satisfacen para un determinado número de valores, conocidos como soluciones o raíces de la ecuación.
Curiosidad
 |
|
|
Aunque ya vimos que la notación que usamos hoy en día para escribir en lenguaje matemático es relativamente actual, las ecuaciones se han resuelto desde la civilización egipcia.
En el Papiro de Rhind (1650 a.C.) se resuelven problemas de un modo análogo al que se usa hoy en día. Uno de los problemas que aparece en este documento es "Un montón y un séptimo del mismo es igual a 24"
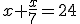
Los babilonios, unos 1000 años después, se centraron básicamente en las ecuaciones de segundo grado; y entre los griegos, que en general se dedicaron a la geometría, debemos destacar la figura de Diofanto de Alejandría (200 a.C. - 284 a.C.). Diofanto publicó en su obra sus estudios acerca de ecuaciones que tienen soluciones racionales. Como curiosidad, has de saber que su epitafio era un problema que se resuelve con una ecuación de primer grado. Dice así:
"Transeúnte, ésta es la tumba de Diofanto: es él quien con esta sorprendente distribución te dice el número de años que vivió. Su niñez ocupó la sexta parte de su vida; después, durante la doceava parte su mejilla se cubrió con el primer bozo. Pasó aún una séptima parte de su vida antes de tomar esposa, y cinco años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle, llorándole, durante cuatro años. De todo esto se deduce su edad."
Este problema se traduce en la siguiente ecuación, siendo x la edad de Diofanto: