4. Traslaciones verticales y horizontales
Ya han transcurrido dos actos y seguro que habrás observado que el decorado ha cambiado entre uno y otro. Cae el telón al finalizar un acto y, cuando vuelve a levantarse, ¡sorpresa! Al levantarse de nuevo vemos que el decorado del escenario ha cambiado completamente o que se transformado, algunos objetos han desaparecido y otros han cambiado de ubicación. Han sido desplazados. Más hacia la derech o izquierda, más hacia arriba o abajo. Tal vez, una mezcla de ambas situaciones.
Las funciones también pueden sufrir transformaciones. Desplazamientos en horizontal en vertical, e incluso cambios de forma.
Del análisis de estas transformaciones nos encargaremos a continuación.
Importante
Trasladar una función, y = f(x), verticalmente k unidades consiste en sumarle a la variable dependiente (y) la constante (k).
Obtenemos así una nueva función: y = f(x) + k
· Si k es positiva, entonces, la función se traslada hacia arriba.
· Si k es negativa, entonces, la función se traslada hacia abajo.
Comprueba lo aprendido
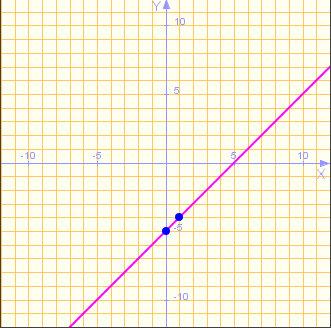
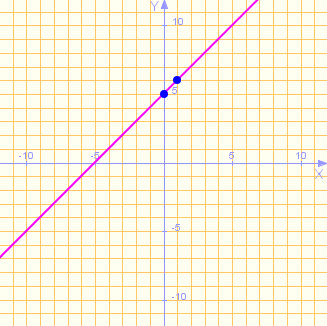
Completa los espacios en blanco relacionados con traslaciones verticales de las funciones afines representadas a continuación:
 |
 |
 |
| Gráfica Nº 1 | Gráfica Nº 2 | Gráfica Nº 3 |
Importante
Trasladar una función, y = f(x), horizontalmente, p unidades consiste en restarle a la variable independiente (x) la constante (p).
Obtenemos así una nueva función: y = f(x-p)
· Si p es positiva, entonces, la función se traslada hacia la derecha.
· Si p es negativa, entonces, la función se traslada hacia la izquierda.
Importante
Si se aplican ambos tipos de transformaciones a f, es decir, una traslación horizontal (de p unidades) más una traslación vertical (de k unidades) es decir, una transformación oblicua, obtendremos la función: y=f(x-p)+k
Para saber más
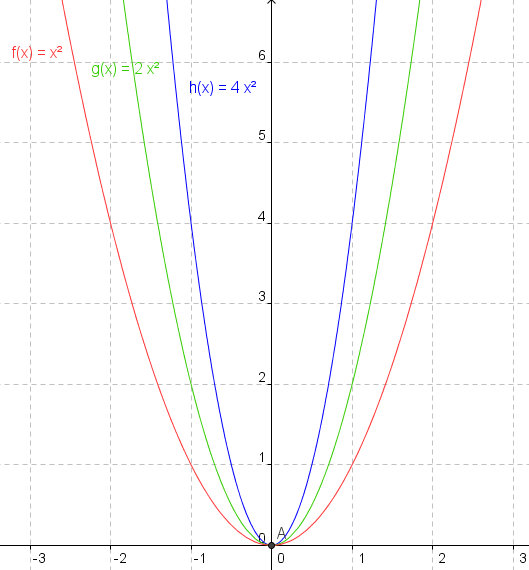
Del mismo modo que las funciones pueden cambiar de lugar, trasladarse, también pueden cambiar de forma, mediante lo que se denominan contracciones o dilataciones.
· Una función, f(x), se contrae si realizamos la siguiente operación: f(k·x) con k > 1
· Una función, f(x), se dilata si realizamos la siguiente operación: f(k·x) con 0 < k < 1
 |
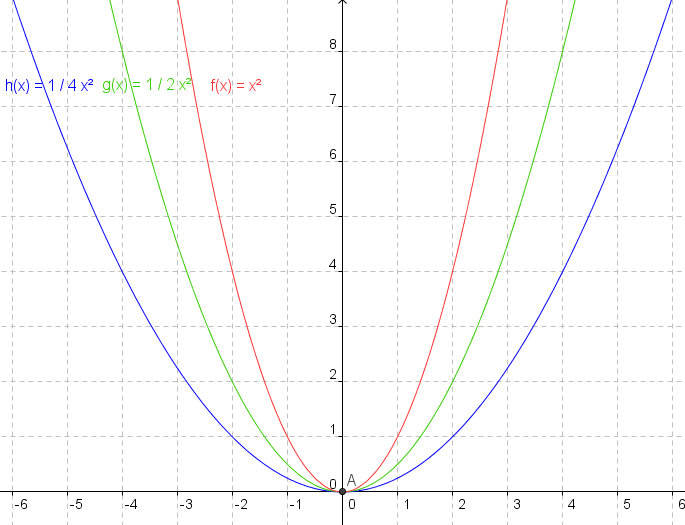 |
| Contracciones | Dilataciones |
Curiosidad
Found Functions.
¿Te gustaría ver gráficas de funciones describiendo y adaptándose perfectamente a la naturaleza, como la que aparece a la izquierda?
Accede a la exposición virtual de Nikki Graziano y disfruta de esta maravilla de trabajo.
