Resumen
Importante
La interpolación es un método que nos permite conocer, aproximadamente, los valores intermedios que toma una función desconocida a partir de datos conocidos.
Importante
Interpolación lineal. El caso más simple que se puede presentar es que se conozcan dos parejas de datos (x1, y1) y (x2, y2). En este caso podemos calcular una función lineal (polinomio de grado 1) f (x)=y=a x+b que cumpla f(x1) = y1 , f(x2) = y2 . Su gráfica es una recta que pasa por los puntos de coordenadas (x1, y1) y (x2, y2) . Una vez obtenida su expresión, dando valores se pueden encontrar nuevos puntos de la función. Los resultados obtenidos son naturalmente estimaciones aproximadas.
Conocidos dos puntos A(x1, y1); B(x2, y2) la función lineal que definen es y=ax+b donde:
![]()
Al coeficiente "a" se le llama pendiente y al "b" ordenada en el origen, como ya viste al trabajar la función lineal en temas anteriores.
Por ejemplo la función lineal que contiene a los puntos A(2,5) y B(4,-1) sería y=-3x+11 ya que
![]()
Importante
A la diferencia entre el valor real (y*) y el estimado (y) se le llama error de interpolación.
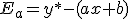
En nuestro ejemplo anterior y*=673.474 e y=674.879, entonces Ea=-1405. La provincia de Badajoz, en el año 2006, tenía 1405 habitantes menos que el valor que hemos hallado en nuestra estimación por interpolación lineal.
Importante
Interpolación cuadrática.Con el fin de minimizar el error de interpolación, cuando tres puntos no están alineados podemos interpolar con una función del tipo y=ax2+bx+c.
A esta interpolación se le llama cuadrática
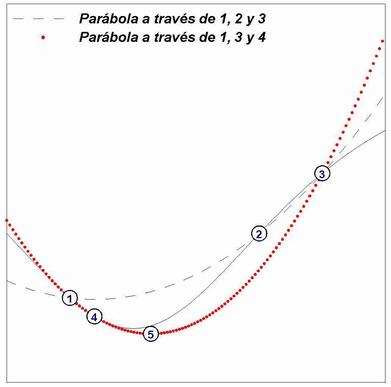 |
Para tres puntos no alineados (x1,y1) (x2,y2) y (x3,y3) la funcion cuadrática que pasa por ellos tiene la expresión:
Importante
Cuando se realiza una estimación para valores que se encuentran fuera del rango (mayores que el máximo o menores que el mínimo) de los datos que poseemos, el proceso se denomina extrapolación.
Este procedimiento conlleva un mayor riesgo de error, al suponer que el comportamiento de la función fuera del intervalo es el mismo que dentro de él.