2.2. Interpolación cuadrática
Importante
Con el fin de minimizar el error de interpolación, cuando tres puntos no están alineados podemos interpolar con una función del tipo y=ax2+bx+c (polinómica de segundo grado). A esta interpolación se le llama cuadrática
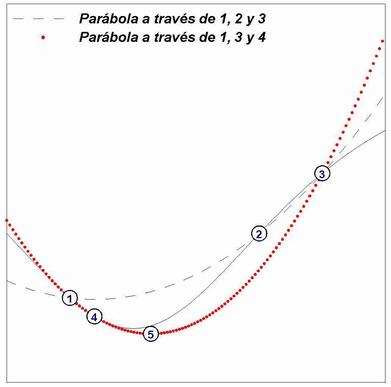 |
Para tres puntos no alineados (x1,y1) (x2,y2) y (x3,y3) la función cuadrática que pasa por ellos tiene la expresión:
Caso práctico
Calcula la función de interpolación cuadrática para los puntos : (0,2), (1,2) y (2,4). Una vez que tengas la expresión de la función obtén el valor de "y" esperado cuando x=1,5.
Comprueba lo aprendido
Marca si es falso o verdad en las cuestiones que se plantean.
Retroalimentación
Falso
Con dos es suficiente
Retroalimentación
Falso
Intenta trazar una recta que pase por Almería, Cáceres y Zaragoza
Retroalimentación
Verdadero
y=3x
Retroalimentación
Verdadero
Para x=3 y*=11 Ea=11-9=2
Importante
Del mismo modo que hacíamos en la interpolación lineal, a la diferencia entre el valor real (y*) y el estimado (y) se le llamará error de interpolación.