2.1. Interpolación lineal

Objetivo

Imagen de madartzgraphics en Pixabay. Pixabay License

Recordemos nuestro objetivo. Queremos encontrar el valor de una función que desconocemos, a partir de datos conocidos. Por lo tanto, vamos a intentar encontrar una función que, aunque no sea exactamente la que buscamos, pero pueda servir para calcular, aproximadamente, otros valores desconocidos de nuestras variables. Lo más lógico es recurrir a las funciones más sencillas que conocemos; las polinómicas.

Importante

Interpolación lineal. El caso más simple que se puede presentar es que se conozcan dos parejas de datos (x1, y1) y (x2, y2). En este caso podemos calcular una función lineal (polinomio de grado 1) f (x)=y=a x+b que cumpla f(x1) = y1 , f(x2) = y2 . Su gráfica es una recta que pasa por los puntos de coordenadas (x1, y1) y (x2, y2) . Una vez obtenida su expresión, dando valores  se pueden encontrar nuevos puntos de la función. Los resultados obtenidos son naturalmente estimaciones aproximadas.
Conocidos dos puntos A(x1, y1); B(x2, y2) la función lineal que definen es y=ax+b donde:

a=\fra{y_2 -y_1}{x_2 -x_1}\ \ \ ;\ \ b=y_1-ax_1

Al coeficiente "a" se le llama pendiente y al "b" ordenada en el origen, como ya viste al trabajar la función lineal en temas anteriores.
Por ejemplo la función lineal que contiene a los puntos A(2,5) y B(4,-1) sería y=-3x+11 ya que

a=\fra{-1 - 5}{4 -2}=\frac {-6}{2}=-3\ \ \ ;\ \ b=5-(-3)\cdot 2=11

En el siguiente vídeo puedes ver un ejemplo de interpolación. Fíjate que utiliza otro método para calcular la recta de interpolación, pero por supuesto igualmente válido.

Vídeo de lasmatematicas alojado en Youtube.

Caso práctico


En un folleto informativo de cierta inmobiliaria presentan la siguiente información:
Venta de pisos desde 60.000 € hasta 120.000 €. El edificio tiene 16 plantas y los precios se encarecen, así lo marca el folleto, con la altura.

¿Cuál es la función lineal definida para los pisos de la 1ª y 16ª?

Importante

Dados tres puntos A(x1 ,y1); B (x2,y2) y C(x3,y3) se dice que están alineados si C pertenece a la recta que pasa por los puntos A y B.
Si y=ax+b es la recta que interpola a A y B , entonces C está alineado con A y B si:  y3=ax3+b.
Por ejemplo, si tenemos los puntos A(-1,2), B(2,9) y C(5,15) para ver si están alineados hallamos la recta que pasa por A y B, que sería y=2x+5, y comprobamos si C pertenece a ella o no, es decir, vemos si verifica la ecuación. En este caso si pertenece ya que 2·5+5 = 15.

Caso práctico


¿Recuerdas la tabla que relacionaba la velocidad de un automóvil con el consumo?

A la izquierda tienes el gráfico en un sistema de ejes. La línea roja que une los puntos dos a dos muestra que al menos tres de ellos no están alineados, ¿podríamos demostrarlo analíticamente?

Por otra parte, la recta que definen los dos últimos puntos (color negro) no pasa por los dos primeros ¿lo probamos también?. Y finalmente ¿Qué consecuencia podemos sacar de la relación de estas dos variables?

Caso práctico


En la siguiente tabla aparecen los habitantes de la provincia de Badajoz:

Año 2005 2007
N.º de habitantes 671.299 678.459

¿Qué población se calcula que tenía en el 2006?

Comprueba lo aprendido

El precio de tres artículos conocidos en dos supermercados distintos del barrio son los que se muestran en la siguiente tabla:

Precio Súper A 10 12 20
Precio Súper B 8 10 18

Contesta verdadero o falso a las cuestiones que se plantean.

Pregunta 1

1.- Dos puntos definen una única recta en el plano.

Pregunta 2

2.-La recta que pasa por los puntos (10,8) y (12,10) es y=x-2

Pregunta 3

3.-Un artículo que en Super A vale 11 €, en el Súper B tiene un valor estimado de 9 €

Pregunta 4

4.-Si en el Súper B el artículo cuesta 16 €, cabe esperar, con los datos de que disponemos, que en el Súper A cueste 14 €

Pregunta 5

5.-Todos los puntos dados en la tabla están alineados

Importante

A la diferencia entre el valor real (y*) y el estimado (y) se le llama error de interpolación.

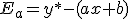
En nuestro ejemplo anterior y*=673.474 e y=674.879, entonces Ea=-1405. La provincia de Badajoz, en el año 2006, tenía 1405 habitantes menos que el valor que hemos hallado en nuestra estimación por interpolación lineal.