3. Fuerza sobre un hilo conductor

Vas a ver ahora un asunto interesante que tiene muchas repercusiones en la práctica. Ya sabes que una corriente eléctrica no es otra cosa que el movimiento de cargas eléctricas en el seno de un conductor. Resulta evidente que, si un campo magnético es capaz de ejercer una fuerza sobre una carga en movimiento, por la misma razón ejercerá una fuerza sobre un conductor por el que circula una corriente eléctrica de intensidad I. 

¿Cuánto vale esa fuerza? Para obtener una fórmula que te permita calcularla, se hará uso de la expresión de la fuerza de Lorentz y con ayuda de algunos "trucos" matemáticos te la presentaré. ¿Preparado? Listo, ¡ya! 

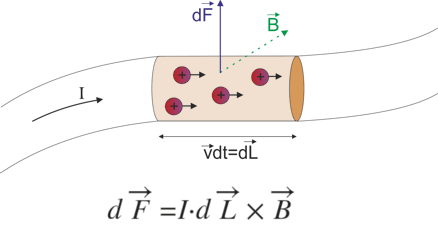Imagen de Juancarcole en Wikimedia Commons. CC

En primer lugar, imagina un trozo de conductor muy, muy pequeño. Tan pequeño, para ahorrar problemas, se pueda suponer que la velocidad de las cargas en él es constante. Los matemáticos y los físicos, como no, llaman a estos trozos tan pequeños elementos infinitesimales. La longitud de este fragmento se representa por dL , al poner la "d" delante se expresa con ello su variación es infinitesimal. Al ser tan diminut, por no decir insignificante, la carga que pasa por ellos en un intervalo de tiempo minúsculo (dt) será también semejante a las otras magnitudes muy reducida (dq). 

La intensidad de corriente, que se define como la carga que atraviesa un punto del conductor en la unidad de tiempo, se expresa como:

por otra parte, para la distancia recorrida por las cargas,  se usa la expresión del movimiento uniforme, recuerda que v es constante en ese trozo.

Bien , ha llegado el momento de aplicar la ley de Lorentz a la carga "dq" que se mueve por el conductor. Si se sustituye ésta por I·dt y, posteriormente, v·dt por dL  queda:

Así que el formalismo matemático de la fuerza ejercida por el campo magnético sobre el trozo "dL" tomo el valor:

Esto está muy bien, sin embargo lo que se desea es conocer la fuerza que actúa sobre un conductor de cierta longitud L que podamos ver, no sobre un trocito imaginario y pequeñísimo dL. ¿Cómo se hace esto? La respuesta es simple, si tenemos un trozo de longitud L, lo que tenemos que hacer es sumar todas las fuerzas dF que actúan sobre los trozos infinitesimales. ¿Y cómo se suma esto? Afortunadamente los matemáticos tienen trucos para casi todo y lo hacen a través de una integral.

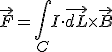
Es posible que ya sepas lo que es una integral, en caso contrario no te preocupes (lo aprenderás este curso en mates), a nosotros lo único que nos interesa es que sepas que, si el conductor es rectilíneo, el resultado de esta integral es:

Esta es la expresión que se quería obtener. Un detalle importante, aunque parece intuitivo, el vector L tiene la dirección y sentido que marca la intensidad de corriente, pero ojo, I no es un vector. No olvides esta fórmula, la utilizarás de nuevo en el apartado siguiente para comprender un fenómeno interesante. De momento, se fragmentará la expresión de la fuerza para su análisis. 

Por ejemplo, se puede empezar escribiendo la expresión del módulo

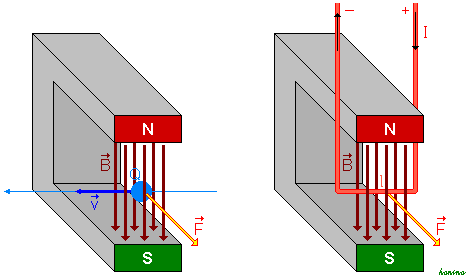
Ya ves que la fórmula es del mismo tipo que la fuerza de Lorentz, es proporcional a la intensidad, la longitud y el campo, y además es perpendicular a L y a B. La dirección y sentido de F la determina el producto vectorial de LxB, la tienes representada en la imagen siguiente. De camino puedes comprobar que también es posible aplicar la regla de la mano izquierda para conocer la dirección y sentido de la fuerza. No olvides que L es un vector que tiene la dirección y sentido de I. 

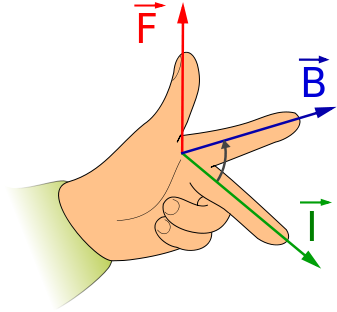Imagen de Honina en Wikimedia Commons. GNU	Imagen de Jfmelero en Wikimedia Commons. CC