2.2 Magnitudes que caracterizan a un mas

Veamos a continuación las magnitudes características de un movimiento armónico simple:

Elongación (x): posición de objeto que vibra o distancia que hay desde donde se encuentra este hasta la posición de equilibrio.

Amplitud (A): valor máximo de elongación.

Periodo (T): tiempo que invierte el cuerpo en realizar un ciclo u oscilación completa (ida y vuelta), esto es, el tiempo que tarda el movimiento en repetirse. Se mide en segundos (s)

Frecuencia (f): número de oscilaciones que el cuerpo realiza en la unidad de tiempo. Se mide en s^-1 o hertzios (Hz). La relación entre la frecuencia y el periodo es: f=1/T

Frecuencia angular (ω): frecuencia expresada en radianes en la unidad de tiempo. Se cumple:

Fase (): el argumento de la función seno Es el valor angular que nos permite calcular la posición del móvil en cualquier instante.

Fase inicial (): valor de la fase en el instante en el que comienza la medida.

Para saber más

Como sabrás, la función seno es periódica y se repite cada ,

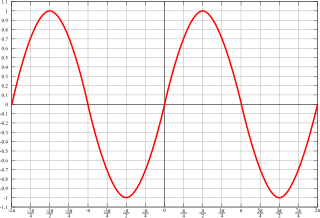Imagen de Keytotime en Wikipedia. CC0

por tanto, el movimiento se repite cuando el argumento de la función seno (ωt+φ₀ ) se incrementa en , es decir, cuando transcurre un tiempo T se cumple:

(\omega (t+T)+\phi _{0})=(\omega t+\phi _{0})+2\pi

Es por ello que: T=2π/ω

Velocidad del MAS

Del MAS sabemos que se trata de un movimiento rectilíneo pero no uniforme porque la velocidad varía. De hecho, puedes ver en la primera animación que el punto verde del muelle se frena cada vez que se acerca a los puntos de máxima separación del punto de equilibrio hasta pararse (pasa de una velocidad máxima en el punto de equilibrio a una velocidad cero en los extremos).

La ecuación de velocidad de un cuerpo con M.A.S. se obtiene derivando la ecuación de posición respecto del tiempo

\[v=\frac{dx}{dt}=Acos(\omega t+\phi _{0})\]

La fórmula de la velocidad en función de la elongación será:

v=\pm \omega \sqrt{A^{2}-x^{2}}

Puedes comprobar que para x = 0 → v = Aω

Por tanto la velocidad máxima se produce en el centro (x = 0) y en los extremos (donde x=A) se cumple que v = 0.

Aceleración del MAS

Derivando la expresión de la velocidad respecto del tiempo obtendremos la aceleración del cuerpo:

a=\frac{dv}{dt}=-A\omega^{2}sen\left ( \omega t +\phi _{0}\right )

Se deduce fácilmente la relación entre la aceleración y la elongación en un MAS:

a=-\omega^{2}x

El valor máximo se alcanza en los extremos de la oscilación, al contrario que la velocidad. Y en el punto medio de equilibrio a = 0, ya que x = 0.

Importante

	ecuación	relación con x	condición de anulación	condición de máximo	valor máximo
velocidad	\[v=Acos(\omega t+\phi _{0})\]	v=\pm \omega \sqrt{A^{2}-x^{2}}	v=0 cuando x=A (en los extremos)	cuando x=0 (en el punto de equilibrio)	\[v_{max}=\omega A\]
aceleración	\[a=-A\omega ^{2}sen(\omega t)\]	a=-\omega^{2}x	a=0 cuando x=0 (en el punto de equilibrio)	cuando x es máxima (en los extremos)	a_{máx}=\omega^2A