2.1 Movimiento armónico simple

El objeto de estudio de este último punto es un movimiento periódico muy característico y de gran interés, el movimiento armónico simple (en adelante, M.A.S.).

Importante

Este es un movimiento de vaivén en el que el cuerpo oscila siguiendo una trayectoria rectilínea. Pasa por el punto medio en cada vibración llegando al máximo y al mínimo, es decir, los extremos, donde el cuerpo se para y vuelve hacia la posición de equilibrio. Esto sucede a intervalos de tiempos iguales. La ecuación que determina la posición del cuerpo es una función senoidal o cosenoidal.

El ejemplo más claro de un MAS es el de un muelle que se estira y se deja oscilar. 

Relación entre el movimiento circular uniforme y el movimiento armónico simple

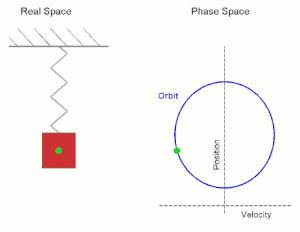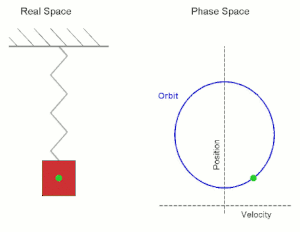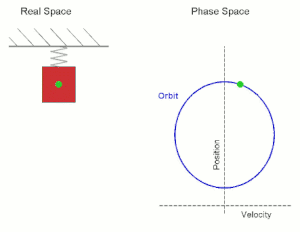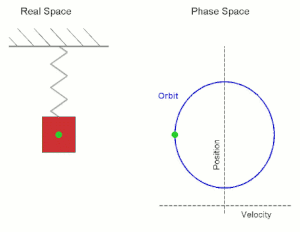
Fíjate en la siguiente animación: en ella puedes ver un objeto (el punto verde) describiendo un movimiento circular. Su movimiento se asemeja al que sigue el cuerpo que cuelga del muelle.

MAS
Imagen de Mazemaster en Wikimedia. CC0   

Se puede constatar que la proyección de un movimiento circular sobre uno de los ejes de coordenadas corresponde a un movimiento armónico simple. 

Con la animación puedes intuir que cuanto mayor es la velocidad del movimiento circular, más rápidas son las oscilaciones de este. 

En la siguiente animación puedes observar de nuevo los dos movimientos.

Varía el radio del MCU y el valor de la frecuencia angular de giro (ω), pulsa sobre el botón de la esquina inferior izquierda y observa qué ocurre con la coordenada  de ambos móviles. Como has podido comprobar, la coordenada  de ambos móviles tienen siempre el mismo valor. El punto azul describe un MCU mientras que el punto verde describe un MAS.Esto es importante ya que a partir de tal situación se puede deducir la ecuación que rige este movimiento.

Animación de Antonio González en Geogebra. CC

Como has podido comprobar, la coordenada  de ambos móviles tienen siempre el mismo valor. El punto azul describe un MCU mientras que el punto verde describe un MAS.

Esto es importante ya que a partir de tal situación se puede deducir la ecuación que rige este movimiento.

Ecuaciones del movimiento armónico simple

¿Cuáles son las ecuaciones del MAS? 

Las ecuaciones de un MCU ya las conocemos:    Recuerda, las coordenadas  e  se pueden escribir en función de R (el radio de giro) y  (el ángulo):
De la imagen, se deduce que

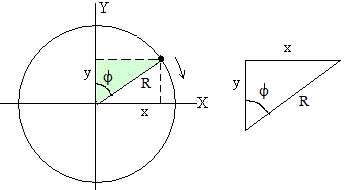x=R\cdot sen\phi

Como la posición cambia con el tiempo, se debe colocar el ángulo en función del tiempo. 

x=R\cdot sen\omega t

Si el movimiento no comienza para un ángulo cero, se ha de añadir un elemento: el desfase .

Quedan por tanto las ecuaciones el MCU:

x=R\cdot sen\phi =R\cdot sen(\omega t+\phi _{0})

y=R\cdot cos\phi =R\cdot cos(\omega t+\phi _{0})

Hemos comprobado, con la segunda animación, que la coordenada  de ambos movimientos coincide, por lo tanto basta tomar la coordenada  del punto rojo para describir el movimiento del punto verde. Esto quiere decir que ya sabemos la ecuación de la posición de un MAS.

Posición en un MAS

Se describe la posición de un objeto que se mueve en el eje X siguiendo un movimiento armónico simple con la siguiente ecuación:

x=Rsen\left (\omega t+\phi _{0} \right )

El valor de la coordenada  es la separación del punto de equilibrio respecto del que oscila nuestro móvil y se denomina elongación. El valor máximo de la elongación se obtiene cuando el seno toma valor 1 o -1:

sen\left ( \omega t+\phi _{0} \right )=\pm 1\Rightarrow x=\pm R

Si llamamos amplitud (A) al valor máximo de la elongación, la ecuación anterior quedará:

x=Asen\left (\omega t+\phi _{0} \right )

Importante

Se puede escribir la ecuación en función del seno o del coseno indistintamente, y esto es gracias a que son expresiones equivalentes, solo se diferencian en la fase inicial (las dos formas simplemente presentan un desfase de π/2) 

Así las expresiones

x=Asen(ωt) 

y

x=Acos(ωt+π/2) 

son equivalentes.