1.2 Movimiento circular uniforme: La velocidad en los móviles que giran
Observa con el siguiente simulador el movimiento de un cuerpo con velocidad angular constante. Modifica el radio de la trayectoria y la velocidad angular para observar distintos movimientos.
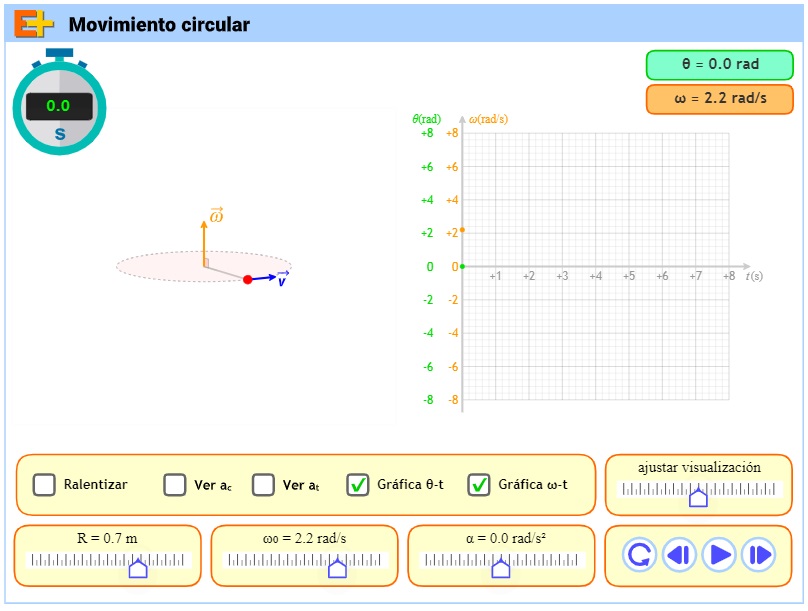Captura de pantalla de animación de Jesús Peñas en Educaplus
| Tiempo (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ángulo (rad) | 0,0 | 3,14 | 6,28 | 9,42 | 12,56 | 15,70 | 18,84 | 21,98 | 25,12 |
Haciendo pruebas con el simulador anterior hemos tomado nota del ángulo (medido en radianes) en diferentes momentos.
Si observas cómo va cambiando el ángulo te darás cuenta de que lo hace a un ritmo constante. Representando el ángulo frente al tiempo podemos comprobarlo definitivamente.
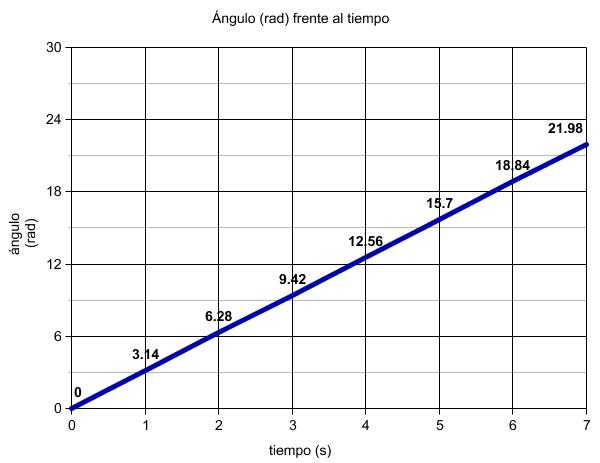
Está claro que en este caso el ritmo de cambio del ángulo es constante y precisamente a eso le debe el nombre el movimiento circular uniforme. Pero, ¿qué magnitud medirá el cambio en el ángulo? La velocidad angular que se mide en radianes por segundo.
\omega =\frac{\varphi_2 - \varphi_1}{t_2-t_1}
En el caso de nuestros datos, obtenemos un valor constante de 3,14 rad/s para la velocidad angular cualquiera que sea el intervalo de tiempo que seleccionemos.
Dado que en los MCU la velocidad angular es constante, podemos calcular podemos calcular el ángulo recorrido en un cierto tiempo operando en la ecuación anterior:
\varphi(t2) - \varphi(t1)=\omega \cdot (t_2-t_1)
Si empezamos a estudiar el movimiento con el cronómetro a cero segundos y sustituimos t2 por t,
\varphi(t) - \varphi_o=\omega \cdot (t-0)
\varphi(t) =\varphi_o + \omega \cdot t
La ecuación de posición en un MCU es:
\varphi(t) = \varphi_o + \omega \cdot t
que recuerda mucho a la ecuación de posición de un MRU pero ahora el papel de las posiciones lo juegan los ángulos y la velocidad angular ha sustituido a la velocidad lineal. Más adelante veremos si existe alguna relación entre estas magnitudes angulares y lineales.
Importante
¿Es la velocidad constante en un MCU?
Ya sabemos que la velocidad de un móvil es una magnitud vectorial y por tanto no basta para describirla con dar el espacio recorrido cada segundo sino que necesitamos indicar la dirección y el sentido con que se mueve. Es decir, la velocidad tiene dos componentes: por un lado su módulo que indica cómo de rápido se mueve el objeto y por otro la dirección y sentido.
En un MRU sabemos que no cambia el módulo de la velocidad porque siempre se mueve con el mismo ritmo y además como la trayectoria es recta, la componente vectorial tampoco. Podemos decir que en un MRU la velocidad, tanto en módulo como en dirección y sentido es constante.
En un MCU sabemos que no cambia el ritmo con que da vueltas pero al describir una circunferencia, la dirección y el sentido cambian continuamente. Por lo tanto, estrictamente la velocidad no es constante es un MCU y cuando decimos que es uniforme queremos decir que el módulo de la velocidad no varía.
Comprueba lo aprendido
Retroalimentación
Verdadero
Retroalimentación
Verdadero
Retroalimentación
Falso
La velocidad de giro se puede expresar en unidades diferentes: vueltas por minuto (rpm, revoluciones por minuto) o por segundo (rps), grados por minuto o por segundo, y radianes por segundo (rad/s), que es la unidad del Sistema Internacional.
Esta magnitud se llama velocidad angular, y se representa por 
. Se calcula como
\omega=\frac{\varphi}{t}
donde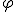 
es el ángulo girado en un tiempo t.
Ejercicio Resuelto
Una lavadora centrifuga a 1200 rpm.
¿Podrías convertir esta velocidad angular a rad/s?
Comprueba lo aprendido
En las siguientes cuestiones necesitarás lápiz y papel, y utilizar las ecuaciones del mcu.
Retroalimentación
Falso
Retroalimentación
Verdadero
Como da 90 vueltas en 30 s, en un segundo da 3 vueltas: es decir,= 3 rps. Pero como una vuelta son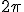 
rad, en total 
rad/s.
Importante
\varphi=\varphi_0+\omega t\\ \omega=constante\\
x= r \cdot cos(\omega t+\varphi_0) \\ y= r \cdot sen(\omega t+\varphi_0)
\vec r= r \cdot cos(\omega t+\varphi_0) \vec i+r \cdot sen(\omega t+\varphi_0) \vec j
Caso práctico
Escribe también la ecuación que nos da el ángulo descrito por la moto en función del tiempo.
Reflexiona
Piensa ahora en la lavadora que tienes en tu casa. El motor gira muy deprisa para que la ropa pierda el agua, que se escapa por los agujeros que tiene el tambor, quedando la ropa escurrida. ¿Qué diferencia práctica habrá entre una muy moderna, que al centrifugar gira hasta a 1600 rpm, frente a las que solamente alcanzan 900 rpm?