1.1 La posición de los móviles que giran
 |
| Imagen de elaboración propia |
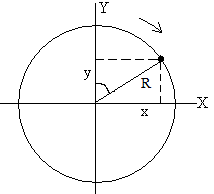
¿Cómo podemos saber dónde se encuentra en un momento concreto un móvil que lleva movimiento circular? Si sabemos situar un punto en el plano, la tarea es sencilla. Recuerda que el vector de posición se puede expresar en función de sus componentes cartesianas.
\vec{r}=x\vec{i}+y\vec{j}
En este caso, el móvil se mantiene siempre a una distancia R del centro de giro, precisamente el radio de la circunferencia que describe. Por eso en este caso particular de trayectoria circular, es más útil utilizar las coordenadas polares. La posición en coordenadas polares se describe utilizando la distancia del punto al origen de coordenadas y el ángulo que forma dicho vector de posición con la parte positiva del eje x.
Ambas descripciones guardan relación. Podemos pasar de las coordenadas 
e 
a las coordenadas polares R y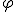 
( se lee fi según la Real Academia de la Lengua) y viceversa. Para ello necesitamos recordar las definiciones de seno y coseno. Tanto el seno como el coseno son razones trigonométricas.
\[cos\varphi =\frac{x}{\left | \overrightarrow{r} \right |}=\frac{x}{\sqrt{x^{2}+y^{2}}}\]
\[sen\varphi =\frac{y}{\left | \overrightarrow{r} \right |}=\frac{y}{\sqrt{x^{2}+y^{2}}}\]
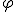: \[x=R\cdot sen\varphi\]
\[y=R\cdot cos\varphi\]
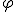podemos determinar e :r=\sqrt{x^{2}+y^{2}}
\varphi = arc cos (\frac{x}{\sqrt{x^{2}+y^{2}}})= arc sen (\frac{y}{\sqrt{x^{2}+y^{2}}})
Importante
La unidad de ángulo en el Sistema Internacional es el radián.
En la descripción de los movimientos circulares también se suelen emplear otras unidades como el grado sexagesimal o la revolución (vuelta).
| Grabación de animación de Jesús Peñas en Educaplus |
Ejercicio Resuelto
Expresa en grados los siguientes ángulos dados en radianes:
rad
rad
rad
rad
En una calculadora científica es muy fácil calcular el seno y el coseno de un ángulo. Por ejemplo imagina que queremos calcular el seno y el coseno de 60º.
Para calcular el seno basta con escribir 60 y luego pulsar la tecla sin. Del mismo modo, pero pulsando la tecla cos, se calcula el coseno.
¿Y al revés? Si sé que el seno de un ángulo 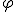es 0,25, ¿cómo puedo calcular dicho ángulo? Pues basta con escribir 0,25 en tu calculadora y luego pulsar las teclas INV y sin sucesivamente.
Caso práctico
Supongamos que tenemos rueda de una bicicleta cuyo radio mide 50 cm. ¿Cuáles son las coordenadas cartesianas y polares de los puntos marcados en la fotografía? Estima aproximadamente los ángulos a partir de la fotografía.
Comprueba lo aprendido
Retroalimentación
Verdadero
Retroalimentación
Verdadero
Retroalimentación
Falso
Retroalimentación
Falso
Importante
Dado que la distancia al centro de giro se mantiene fija en los movimientos circulares, vamos a utilizar coordenadas polares para describirlo. Daremos la distancia al centro y el ángulo entre el lado positivo del eje x y el vector de posición de nuestro móvil.