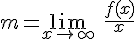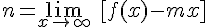Resumen
Importante
Supongamos que tenemos una función f(x) y dos valores a y L. La idea intuitiva nos dice que el límite de la función f(x) es L cuando la variable x tiende al valor a si, a medida que vamos dándole a x valores más cercanos al valor a, la función va tomando valores más cercanos al valor L.
La forma de expresarlo es 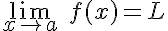
En general, a la hora de calcular el límite de una función en un punto, es suficiente con sustituir el valor en la función. Si obtenemos un valor real, ése es el límite de la función. Si obtenemos algún valor indeterminado o infinito entonces hay que trabajar de distinta manera. En el tema siguiente veremos el cálculo de límites de una manera más rigurosa.
Importante
Llamaremos límite por la derecha de la función f(x) al valor que se obtiene en la función cuando x se acerca al valor a por la derecha, es decir siempre por valores mayores que a. Se representa por
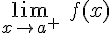
Hablaremos del límite de la función f(x) cuando x tiende al valor a por la izquierda a lo que se obtiene cuando a x le vamos dando valores cercanos al valor a por la izquierda, es decir, manteniéndose siempre por valores más pequeños. Se representa por
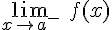
Importante
La condición para que exista el límite de una función en un punto es que existan los dos límites laterales y que coincidan. Si los límites laterales no coinciden entonces no existe el límite de la función en el punto. Se tiene por tanto:
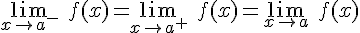
Importante
Dada la función f(x) diremos que la recta de ecuación x=a es una asíntota vertical si se verifica

Importante
Diremos que la función f(x) tiene una asíntota horizontal y=b si la función tiende hacia b a medida que la variable tiende a infinito. Es decir, cuando se verifica
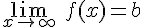
Importante
Lllamaremos asíntota oblicua de una función f(x) a una recta, de ecuación 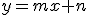 , con la que la función tiende a coincidir en el infinito.
, con la que la función tiende a coincidir en el infinito.
Para calcularla se utilizan las siguientes igualdades: