2. Funciones polinómicas
 |
|
|
Os confieso que mi caída del árbol fue aterradora. Me parecía ir a una gran velocidad, sobre todo comparada con la de las hojas que cayeron conmigo ¡Cómo habrían cambiado las cosas si me hubiese caído dentro de una campana como ésta! Entonces habríamos caído todas con una velocidad ![]() normal y corriente...
normal y corriente...
Siempre fui una manzana un poco rara: me gustaba observar este tipo de cuestiones. Ver cómo un gorrión volaba hacia su nido a unos 2 metros por segundo y determinar que el espacio que recorría seguía la función f(x)=2x (donde por supuesto x es el tiempo que está volando). O verlo parado en una rama, atento al movimiento de cualquier insecto con el que alimentar a sus polluelos, y lanzarse a por él acelerando a 10 m/s2. En este caso el espacio que recorre es g(x)=5x2.
¿Qué ocurre si unimos los dos casos? Tendremos un gorrión que parte de una velocidad de 2m/s y que acelera a 10m/s2. El espacio que recorre será la suma de los dos casos anteriores: h(x)=f(x)+g(x)=2x+5x2.
Importante
Si tenemos dos funciones reales f(x) y g(x), las funciones s(x)=f(x)+g(x) y r(x)=f(x)-g(x) obtenidas al sumar o restar f y g, también son funciones reales.
Ejercicio Resuelto
En la siguiente escena de GeoGebra puedes ver las gráficas de las funciones lineales f(x)=-x+8 y g(x)=2x-4. Al mover el punto verde, que está situado en el origen de coordenadas, irá apareciendo la gráfica de la función f(x)+g(x). A la derecha de la escena puedes ver cómo va variando el valor de x, f(x), g(x) y f(x)+g(x).
a) ¿Cuánto vale (f+g)(4)?
b) ¿Cuál es la expresión analítica de f(x)+g(x)? ¿Qué tipo de función es?
c) ¿Para qué valor de x (f+g)(x)=0?
Importante
Si tenemos dos funciones reales f(x) y g(x), la función p(x)=f(x)·g(x) obtenida al multiplicar f y g, también es una función real.
Reflexiona
En estos tres casos que acabamos de ver (función suma, resta y producto), el dominio será la intersección de los dominios de f y g.
Si te fijas en el caso anterior, hemos multiplicado dos funciones lineales f(x)=x y g(x)=3x+1, y el resultado es una función cuadrática h(x)=3x2+x, pues estamos multiplicando dos polinomios de primer grado para obtener uno de segundo grado.
Si multiplicas una función lineal por una cuadrática, el resultado será un polinomio de tercer grado y de esta forma podrás seguir obteniendo funciones que serán polinomios del grado que quieras.
Importante
Una función de la forma f(x)=anxn+an-1xn-1+...+a2x2+a1x+a0 donde n es un número natural, a0, a1, ... , an son números reales y an es distinto de cero, se llama función polinómica de grado n.
¡Claro que no nos podíamos parar en las funciones cuadráticas! Hay funciones polinómicas de tercer, cuarto, quinto grado, etc. No nos detendremos a estudiar sus características, pues hay una gran variedad, pero si te daremos unas nociones básicas que debes saber:
- El dominio de cualquier función polinómica es todo el conjunto de los números reales.
- El recorrido de una función polinómica de grado impar es todo el conjunto de los números reales.
- Siempre se pueden dibujar de un sólo trazo.
- Como máximo, cortan al eje OX en n puntos.
- Tienen, a lo sumo, n-1 máximos o mínimos relativos.
- Como máximo, tienen n-2 puntos de inflexión.
Aquí tienes unos ejemplos:
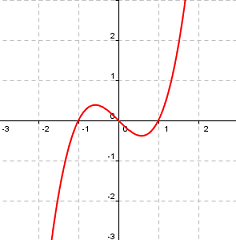 |
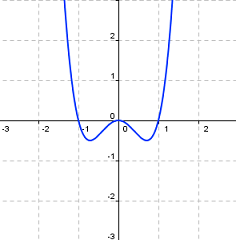 |
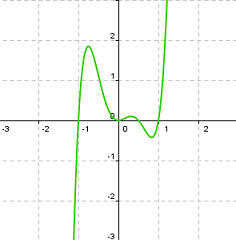 |
|
Función polinómica de grado 3 f(x)=x3-x |
Función polinómica de grado 4 g(x)=2x4-2x2 |
Función polinómica de grado 5 h(x)=6x5-3x4-6x3+3x2 |
Si quieres representar una función polinómica, a continuación tienes los pasos que puedes seguir.